
2.如图,正三棱柱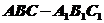 的所有棱长都为2,
的所有棱长都为2,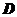 为
为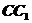 中点,试用空间向量知识解下列问题:
中点,试用空间向量知识解下列问题:
(1)求证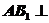 面
面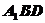 ;
;
(2)求二面角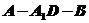 的大小。
的大小。
1.某商品,根据以往资料统计,顾客采用的付款期数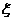 的分布列为
的分布列为
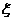 |
1 |
2 |
3 |
4 |
5 |
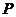 |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.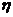 表示经销一件该商品的利润.(1)求事件
表示经销一件该商品的利润.(1)求事件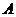 :“购买该商品的3位顾客中,至少有1位采用1期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率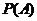 ;(2)求
;(2)求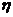 的分布列及期望
的分布列及期望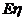 .
.
20.已知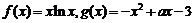 .
.
(Ⅰ) 求函数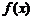 在
在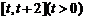 上的最小值;
上的最小值;
(Ⅱ) 对一切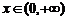 ,
,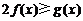 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(Ⅲ) 证明: 对一切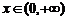 ,都有
,都有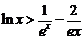 成立.
成立.
(理科加试部分)
19.设正项数列{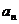 }的前项和为Sn,q为非零常数。已知对任意正整数n, m,当n > m时,
}的前项和为Sn,q为非零常数。已知对任意正整数n, m,当n > m时,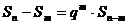 总成立。
总成立。
(1)求证数列{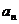 }是等比数列; (2)若正整数n, m, k成等差数列,求证:
}是等比数列; (2)若正整数n, m, k成等差数列,求证: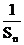 +
+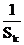 ≥
≥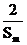 .
.
18.已知矩形纸片ABCD中,AB=6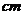 ,AD=12
,AD=12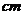 ,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设
,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设

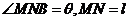 。
。
(1)试将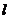 表示成
表示成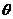 的函数;(2)求
的函数;(2)求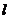 的最小值。
的最小值。
17.抛物线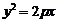 的准线的方程为
的准线的方程为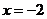 ,该抛物线上的每个点到准线
,该抛物线上的每个点到准线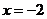 的距离都与到定点N的距离相等,圆N是以N为圆心,同时与直线
的距离都与到定点N的距离相等,圆N是以N为圆心,同时与直线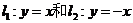 相切的圆,
相切的圆,
(Ⅰ)求定点N的坐标;(Ⅱ)是否存在一条直线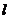 同时满足下列条件:①
同时满足下列条件:① 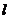 分别与直线
分别与直线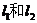 交于A、B两点,且AB中点为
交于A、B两点,且AB中点为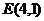 ;②
;② 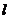 被圆N截得的弦长为
被圆N截得的弦长为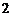 .
.

|
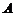 、
、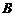 是单位圆
是单位圆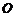 上的点,
上的点,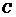 是圆与
是圆与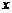 轴正半轴的交点,
轴正半轴的交点, 点的坐标为
点的坐标为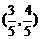 ,三角形
,三角形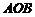 为正三角形.
为正三角形.
(1)求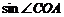 ;(2)求
;(2)求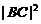 的值.
的值.
16.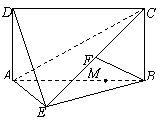 如图,四边形ABCD为矩形,AD⊥平面ABE,
如图,四边形ABCD为矩形,AD⊥平面ABE, 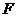 为
为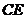 上的点,且BF⊥平面ACE.
上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;(2)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.
14、函数f(x)=|x2-a|在区间[-1,1]上的最大值为M(a),则M(a)的最小值是___▲___
13.若 为
为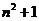
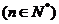 的各位数字之和,如
的各位数字之和,如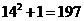 ,
,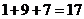 ,
,
则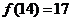 ;记
;记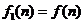 ,
,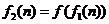 ,…,
,…,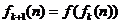 ,
,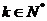 ,则
,则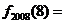 ▲ ;
▲ ;
12. 在单位正方体
在单位正方体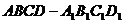 的面对角线
的面对角线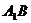 上存在一点
上存在一点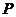
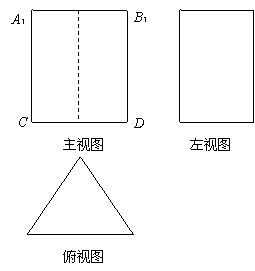 使得
使得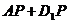 最短,则
最短,则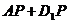 的最小值为 .
的最小值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com