
6、、读下面这首诗,完成1-2题。(6分)
清溪行
李白
清溪清我心,水色异诸水。
借问新安江,见底何如此?
人行明镜中,鸟度屏风里。
向晚猩猩啼,空悲远游子。
[注]本诗是天宝十二载(753)秋后李白游池州(治所在今安徽贵池)时所作。
1.诗人以 手法侧面表现清溪水色的清澈,又以 的手法正面表现清溪的清澈。(每空1分,共2分)
2.有人说这首诗的诗眼是“清”字,你同意吗?请结合全诗作简要分析。(4分)
[答案]1.对比衬托;比喻(2分)
2.同意,“清溪清我心”,诗人一开始就描写了自己的直接感受,清溪的水色给他以清心的感受,点明了水色的特异之处。(1分),二、三两联用反衬比喻等手法着力描写了清溪的清溪的清澈美丽,营造了一种明净纯澈的意境(1分)最后又创造了一个情调凄凉的清寂境界,(1分)诗人在这美丽的清溪畔,固然清心,但听到猩猩的一声声啼叫,似乎在为自己远游他乡而悲切,流露出诗人内心一种落寞悒郁的情绪。 (1分)
[赏析]
这是一首情景交融的抒情诗,是天宝十二载(753)秋后李白游池州(治所在今安徽贵池)时所作。池州是皖南风景胜地,而风景名胜又大多集中在清溪和秋浦沿岸。清溪源出石台县,象一条玉带,蜿蜒曲折,流经贵池城,与秋浦河汇合,出池口泻入长江。李白游清溪写下了好多有关清溪的诗篇。这首《清溪行》着意描写清溪水色的清澈,寄托诗人喜清厌浊的情怀。
“清溪清我心”,诗人一开始就描写了自己的直接感受。李白一生游览过多少名山秀川,独有清溪的水色给他以清心的感受,这就是清溪水色的特异之处。
接着,诗人又以衬托手法突出地表现清溪水色的清澈。新安江源出徽州,流入浙江,向以水清著称。南朝梁沈约就曾写过一首题为《新安江水至清浅深见底贻京邑游好》的诗:“洞彻随深浅,皎镜无冬春。千仞写乔树,百丈见游鳞。”新安江水无疑是清澈的,然而,和清溪相比又将如何呢?“借问新安江,见底何如此?”新安江那能比得上清溪这样清澈见底呢!这样,就以新安江水色之清衬托出清溪的更清。
然后,又运用比喻的手法来正面描写清溪的清澈。诗人以“明镜”比喻清溪,把两岸的群山比作“屏风”。你看,人在岸上行走,鸟在山中穿度,倒影在清溪之中,就如:“人行明镜中,鸟度屏风里。”这样一幅美丽的倒影,使人如身入其境。胡仔云:“《复斋漫录》云:山谷言:”船如天上坐,人似镜中行。‘又云:“船如天上坐,鱼似镜中悬。’沈云卿诗也。……予以云卿之诗,原于王逸少《镜湖》诗所谓‘山阴路上行,如坐镜中游’之句。然李太白《入青溪山》亦云:”人行明镜中,鸟度屏风里。‘虽有所袭,然语益工也。“(《苕溪渔隐丛话》)
最后,诗人又创造了一个情调凄凉的清寂境界。诗人离开混浊的帝京,来到这水清如镜的清溪畔,固然感到“清心”,可是这对于我们这位胸怀济世之才的诗人,终不免有一种心灵上的孤寂。所以入晚时猩猩的一声声啼叫,在诗人听来,仿佛是在为自己远游他乡而悲切,流露出诗人内心一种落寞悒郁的情绪。
|
直线名称 |
已知条件 |
直线方程 |
使用范围 |
示意图 |
|
点斜式 |
 |
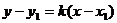 |
 |
|
|
斜截式 |
 |
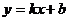 |
 |
|
|
两点式 |
 ( (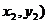 |
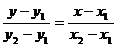 |
 |
|
|
截距式 |
 |
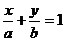 |
 |
|
设计意图:为帮助学生用联系的观点来学习知识,又能把四种形式的直线方程加以区别,以便更好地运用它们,本环节主要采用比较法的形式小结
(1)过点P(2,1)作直线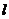 交
交 正半轴于AB两点,当
正半轴于AB两点,当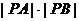 取到最小值时,求直线
取到最小值时,求直线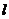 的方程.
的方程.
解:设直线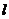 的方程为:
的方程为:
令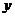 =0解得
=0解得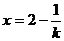 ;令
;令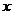 =0,解得
=0,解得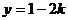
∴A(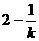 ,0),B(0,
,0),B(0,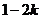 ),
),
∴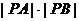 =
=
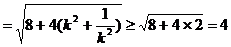
当且仅当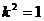 即
即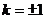 时,
时,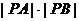 取到最小值.
取到最小值.
又根据题意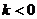 ,∴
,∴
所以直线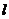 的方程为:
的方程为: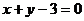

评述:此题在求解过程中运用了基本不等式,同时应注意结合直线与坐标轴正半轴相交而排除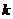 =1的情形
=1的情形
(2)一直线被两直线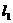 :
: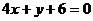 ,
, :
: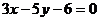 截得的线段的中点恰好是坐标原点,求该直线方程.
截得的线段的中点恰好是坐标原点,求该直线方程.
解:设所求直线与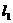 ,
, 的交点分别是A、B,设A(
的交点分别是A、B,设A( ),则B点坐标为(
),则B点坐标为( )
) 
因为A、B分别在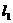 ,
, 上,所以
上,所以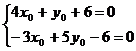
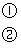
①+②得: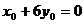 ,即点A在直线
,即点A在直线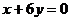 上,又直线
上,又直线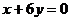 过原点,所以直线
过原点,所以直线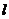 的方程为
的方程为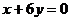 .
.
(3)直线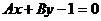 在
在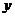 轴上的截距是-1,而且它的倾斜角是直线
轴上的截距是-1,而且它的倾斜角是直线 的倾斜角的2倍,则( )
的倾斜角的2倍,则( )
A. A= ,B=1 B.A=-
,B=1 B.A=- ,B=-1
,B=-1
C.A= ,B=-1 D.A=-
,B=-1 D.A=- ,B=1
,B=1
解:将直线方程化成斜截式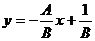 .
.
因为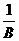 =-1,B=-1,故否定A、D.
=-1,B=-1,故否定A、D.
又直线 的倾斜角
的倾斜角 =
=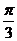 ,
,
∴直线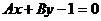 的倾斜角为2
的倾斜角为2 =
= ,
,
∴斜率- =-
=-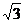 ,
,
∴A=-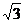 ,B=-1,故选B
,B=-1,故选B
(4)若直线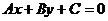 通过第二、三、四象限,则系数A、B、C需满足条件( )
通过第二、三、四象限,则系数A、B、C需满足条件( )
A.A、B、C同号 B.AC<0,BC<0 C.C=0,AB<0 D.A=0,BC<0
解法一:原方程可化为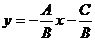 (B≠0)
(B≠0)
∵直线通过第二、三、四象限,
∴其斜率小于0,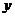 轴上的截距小于0,即-
轴上的截距小于0,即- <0,且-
<0,且- <0
<0
∴ >0,且
>0,且 >0
>0
即A、B同号,B、C同号.∴A、B、C同号,故选A
解法二:(用排除法)
若C=0,AB<0,则原方程化为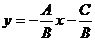 =-
=-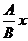 .
.
由AB<0,可知- >0.
>0.
∴此时直线经过原点,位于第一、三象限,故排除C.
若A=0,BC<0,则原方程化为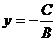 .由BC<0,得-
.由BC<0,得- >0.
>0.
∴此时直线与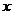 轴平行,位于
轴平行,位于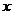 轴上方,经过一、二象限.故排除D.
轴上方,经过一、二象限.故排除D.
若AC<0,BC<0,知A、C异号,B、C异号
∴A、B同号,即AB>0.
∴此时直线经过第一、二、四象限,故排除B.故A、B、C同号,应选A
(5)直线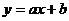 (
(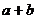 =0)的图象是( )
=0)的图象是( )
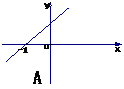


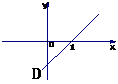
解法一:由已知,直线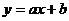 的斜率为
的斜率为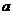 ,在
,在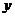 轴上的截距为
轴上的截距为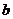

又因为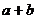 =0.
=0.
∴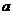 与
与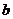 互为相反数,即直线的斜率及其在
互为相反数,即直线的斜率及其在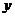 轴上的截距互为相反数
轴上的截距互为相反数
图A中,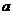 >0,
>0,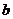 >0;图B中,
>0;图B中,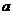 <0,
<0,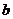 <0;图C中,
<0;图C中,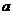 >0,
>0,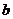 =0
=0
故排除A、B、C.选D.
解法二:由于所给直线方程是斜截式,所以其斜率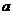 ≠0,于是令
≠0,于是令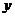 =0,解得
=0,解得 .又因为
.又因为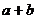 =0,∴
=0,∴ ,∴
,∴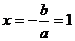
∴直线在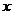 轴上的截距为1,由此可排除A、B、C,故选D
轴上的截距为1,由此可排除A、B、C,故选D 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com