4.复数为纯虚数，则实数a= DA．0　 B．－4　 C．－6　　　　 D．－8

3.从1，2，3，4，7，9这六个数，任取两个分别作为一个对数的底数和真数，则可以组成的不同的对数值的个数A

A.17　　　　　　　 B.19　　　　 C.21　　　　　　　 D.23

2..如果ab<0，a+b=1，且二项式(a+b)³按a的降幂展开后，第二项不大于第三项，则a的取值范围是(　　 ).D

A.(-∞，-　　　　　　 B.[,+∞　　 C.(-∞，+　　 D.(1，+∞)

1..已知(2x²+4x+3)⁶=a₀+a₁(x+1)²+a₂(x+1)⁴+…+a₆(x+1)¹²，则a₀+a₂+a₄+a₆的值为BA. B. 　C. 　D.

19．(Ⅰ)证明：如图，连结B₁C交BC₁于F，连结DE、DF.则由题设可知：EF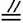

而A₁D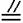　 ∴EF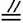A₁D∴四边形A₁DFE为平行四边形.∴A₁E//DF.又DF平面DBC₁，A₁E面DBC₁，

∴A₁E//面DBC₁.

(Ⅱ)(理)取BC的中点F，连结EF交BC₁于点O，则O为BC₁的中点.

过M作MN//A₁E交OE于点N，则.

∵A₁E⊥面B₁BCC₁，

∴MN⊥面B₁BCC₁.

∴过N作NR⊥BC₁交BC₁于R，连结MR，则∠MRN为二面角M-BC₁-B₁的平面角.(8分)

要使

显然说明点M在AA₁的延长线上，同理，在A₁A的延长线上也存在一点P，得.

　 在A₁A所在直线上存在点M，使二面角M-BC₁-B₁成60°.且AP=2+或

(3)如图(1)，过E作EP⊥BC₁，连结A₁P.

由题意知，∽

22.本小题主要考查函数和不等式的概念，考查数学归纳法，以及灵活运用数学方法分析和

解决问题的能力..

(1)解：由于的最大值不大于所以

　　 　　　　①　

又所以.　 ②

由①②得

(2)证法二：(i)当n=1时，，不等式成立；

(ii)假设时不等式成立，即，则当n=k+1时，

因所以

于是　 因此当n=k+1时，不等式也成立.

根据(i)(ii)可知，对任何，不等式成立.

22.已知函数的最大值不大于，又当

　 (1)求a的值；(2)设

21、A袋中有1张10元1张5元的钱币，B袋中有2张10元1张5元的钱币，从A袋中任取一张钱币与B袋任取一张钱币互换，这样的互换进行了一次.求 (1) 　A袋中10元钱币恰是一张的概率；(2) 设A袋中的期望金额为a元，求a .

20．已知函数 (1)画出函数的图像； 　(2)证明函数在x=1 处连续．

19．如图，D、E分别是正三棱柱ABC-A₁B₁C₁的棱AA₁、B₁C₁的中点，且棱AA₁=4，AB=2.

(1)求证：A₁E//面BDC₁；

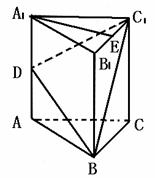　 (2)在棱A₁A所在直线上是否存在一点M，使二面角M-BC₁-B₁成60°.若存在，求出AM的长；若不存在，说明理由.

(3)求二面角A₁-BC₁-B₁的正切值.