
9、如图,函数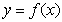 的图象在点P处的切线是
的图象在点P处的切线是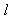 ,
,
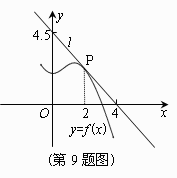 则
则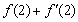 = ▲
;
= ▲
;
8、已知偶函数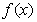 在
在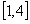 上单调递增,则
上单调递增,则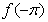 ▲
▲ 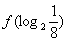 ;(填“
;(填“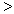 ”、“
”、“ ”或“=”)
”或“=”)
7、若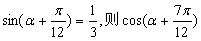 的值为 ▲
;
的值为 ▲
;
6、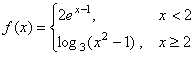 ,则
,则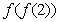 = ▲ ;
= ▲ ;
5、用二分法求方程 x3 −2x −5 = 0在区间(2,3)上的近似解,取区间中点 ,那么下一个有解区间为 ▲ ;
,那么下一个有解区间为 ▲ ;
4、“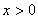 ”是“
”是“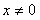 ”的 ▲
条件;(填“充分不必要”、“必要不充分”、“充要”
”的 ▲
条件;(填“充分不必要”、“必要不充分”、“充要”
或“既不充分也不必要”)
3、复数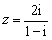 (
(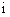 为虚数单位)的实部是 ▲ ;
为虚数单位)的实部是 ▲ ;
2、命题:“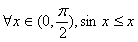 ”的否定是
▲
;
”的否定是
▲
;
1、集合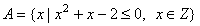 ,则集合A中所有元素之积为 ▲ ;
,则集合A中所有元素之积为 ▲ ;
22.解法一:(1)取BC的中点H,连EH,易得EH是EF在平面AC上的射影,
∵BD⊥EH,∴由三垂线定理,得 EF⊥BD;
又∵EF在平面AB1上的射影是B1E,由△BB1E∽△ABG,得B1E⊥BG,∴由三垂线定理,得 EF⊥BG,
∵BG∩BD=B,∵EF⊥平面GBD.
(2)取C1D1的中点M,连EM,易得EM∥AD1,所以∠EFM就是异面直线AD1与EF所成的角,
∵MF∥BD,∴EF⊥MF .在Rt△EFM中,由EM= ,(a为正方体的棱长),EF=
,(a为正方体的棱长),EF= ,得
,得
∠EFM=30º.即异面直线AD1与EF所成的角为30º.
解法二:(向量法)(1) 以AD为x轴,DC为y轴,DD1为z轴建立空间坐标系,不妨设正方体的棱长为2,
则D(0,0,0),A(2,0,0),B(2,2,0),E(2,1,0),F(1,2,2),G(2,,0,1) ,D1(0,0,2 )
∵ (2,2,0)·(1,-1,-2)=0,
(2,2,0)·(1,-1,-2)=0, (0,-2,1)·(1,-1,-2)=0
(0,-2,1)·(1,-1,-2)=0
∴ ,
, ,又∵BG∩BD=B,∵EF⊥平面GBD.
,又∵BG∩BD=B,∵EF⊥平面GBD.
(2) =(-2,0,2),
=(-2,0,2), =(1,-1,-2) .
=(1,-1,-2) .  =
= ,
,
即异面直线AD1与EF所成的角为30º.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com