
2.y=ln2x+2lnx+2的极小值为( ) A.e-1 B.0 C.-1 D.1
1.函数y=x3-3x的极大值为m,极小值为n,则m+n为( )
A.0 B.1 C.2 D.4
1.3.2利用导数研究函数的极值
(第一课时)
|
学习目标: 掌握求可导函数的极值的步骤  学习重点难点: 掌握求可导函数的极值的步骤  自主学习 一、知识回顾: 1. 函数的导数与函数的单调性的关系:设函数y=f(x) 在某个区间内有导数,如果在这个区间内 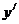 >0,那么函数y=f(x) 在为这个区间内的增函数;如果在这个区间内 >0,那么函数y=f(x) 在为这个区间内的增函数;如果在这个区间内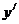 <0,那么函数y=f(x) 在为这个区间内的减函数 <0,那么函数y=f(x) 在为这个区间内的减函数  2.用导数求函数单调区间的步骤:①求函数f(x)的导数f′(x). ②令f′(x)>0解不等式,得x的范围就是递增区间.③令f′(x)<0解不等式,得x的范围,就是递减区间  二、新课探究 1.极大值: 一般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)<f(x0),就说f(x0)是函数f(x)的一个极大值,记作y极大值=f(x0),x0是极大值点  2.极小值:一般地,设函数f(x)在x0附近有定义,如果对x0附近的所有的点,都有f(x)>f(x0).就说f(x0)是函数f(x)的一个极小值,记作y极小值=f(x0),x0是极小值点  3.极大值与极小值统称为极值  在定义中,取得极值的点称为极值点,极值点是自变量的值,极值指的是函数值  请注意以下几点: 请注意以下几点:(ⅰ)极值是一个局部概念  由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小 由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小 并不意味着它在函数的整个的定义域内最大或最小 并不意味着它在函数的整个的定义域内最大或最小 (ⅱ)函数的极值不是唯一的  即一个函数在某区间上或定义域内极大值或极小值可以不止一个 即一个函数在某区间上或定义域内极大值或极小值可以不止一个 (ⅲ)极大值与极小值之间无确定的大小关系  即一个函数的极大值未必大于极小值,如下图所示, 即一个函数的极大值未必大于极小值,如下图所示,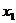 是极大值点, 是极大值点, 是极小值点,而 是极小值点,而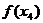 > >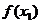  (ⅳ)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点  而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点 而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点 4. 判别f(x0)是极大、极小值的方法: 若 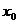 满足 满足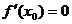 ,且在 ,且在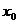 的两侧 的两侧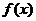 的导数异号,则 的导数异号,则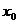 是 是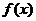 的极值点, 的极值点,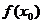 是极值,并且如果 是极值,并且如果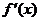 在 在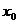 两侧满足“左正右负”,则 两侧满足“左正右负”,则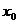 是 是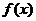 的极大值点, 的极大值点,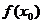 是极大值;如果 是极大值;如果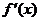 在 在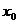 两侧满足“左负右正”,则 两侧满足“左负右正”,则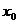 是 是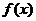 的极小值点, 的极小值点,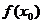 是极小值 是极小值 5. 求可导函数f(x)的极值的步骤: (1)确定函数的定义区间,求导数f′(x)  (2)求方程f′(x)=0的根  (3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查f′(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右不改变符号,那么f(x)在这个根处无极值  三、例题解析: 例1求y= 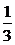 x3-4x+4的极值 x3-4x+4的极值 解:y′=( 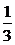 x3-4x+4)′=x2-4=(x+2)(x-2) x3-4x+4)′=x2-4=(x+2)(x-2)
 令y′=0,解得 令y′=0,解得x1=-2,x2=2  当x变化时,y′,y的变化情况如下表 当x变化时,y′,y的变化情况如下表
值且y极小值=- 例2求y=(x2-1)3+1的极值 解:y=6x(x2-1)2=6x(x+1)2(x-1)2令y′=0解得x1=-1,x2=0,x3=1 当x变化时,y′,y的变化情况如下表
∴当x=0时,y有极小值且y极小值=0
求极值的具体步骤:第一,求导数f′(x).第二,令f′(x)=0求方程的根,第三,列表,检查f′(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值,如果左右都是正,或者左右都是负,那么f(x)在这根处无极值.如果函数在某些点处连续但不可导,也需要考虑这些点是否 是极值点 课堂巩固: 21.[浙江省富阳新中2008(上)高三期中考试数学(理科)试卷第22题] (本小题满分15分) 设函数 (Ⅰ)若 (Ⅱ)如果 (Ⅲ)是否存在最小的正整数 20. [广东省海珠区2009届高三综合测试二理科数学第21题](本小题满分14分) 已知 (Ⅰ)求函数 (Ⅱ)求函数 (Ⅲ)对一切的 19.[浙江省嘉兴市2008学年高中学科基础测试数学(理科)试卷第20题] (本小题满分14分) 已知函数
(Ⅰ)若函数f(x)的图象在x=2处的切线方程为 (Ⅱ)若函数f(x)在(1,+∞)为增函数,求a的取值范围. 18.[福建莆田一中2008-2009学年期中考试卷高三数学(理科)第11题] 若 A. C. 17.[福建莆田一中2008-2009学年期中考试卷高三数学(理科)] 已知 范围是( )
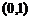 B.
B.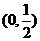 C.
C.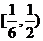 D.
D.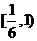 16、[江苏南京二中2009届高三第一次教学质量检测试卷数学第6题] 函数 A. 15、[福建莆田一中2008-2009学年期中考试卷高三数学(文科)第8题] 设函数f(x)= A.(- C.(-1,0) 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |