
2. 美丽的“水立方”(Water Cube)是北京奥运会游泳馆,设计灵感来自于有机细胞的天然图案以及肥皂泡的形成。在这个中心的蓝色汽泡墙之内,钢结构的基本单位是一个由 12 个正五边形和2个正六边形所组成的几何细胞。覆盖这个框架的是半透明的汽泡,称为PTFE膜(聚四氟乙烯),它能为场馆内带来更多的自然光。根据以上信息,下列说法不正确的是
美丽的“水立方”(Water Cube)是北京奥运会游泳馆,设计灵感来自于有机细胞的天然图案以及肥皂泡的形成。在这个中心的蓝色汽泡墙之内,钢结构的基本单位是一个由 12 个正五边形和2个正六边形所组成的几何细胞。覆盖这个框架的是半透明的汽泡,称为PTFE膜(聚四氟乙烯),它能为场馆内带来更多的自然光。根据以上信息,下列说法不正确的是
A.若设想将一个结构单元钢棍焊成足球形状“碳笼”,它与C24形状相似
B.若设想将一个结构单元钢棍焊成足球形状“碳笼”,需钢棍(相当于键)36 根
C.PTFE的单体为:CF2=CF2
D.PTFE在空气中易被氧气氧化
1.化学与科学、技术、社会、环境密切相关。下列有关说法中错误的是
A.国庆60周年燃放的焰火是某些金属元素焰色反应所呈现出来的色彩
B.加热能杀死甲型H1N1流感病毒是因为病毒的蛋白质受热变性
C.含磷洗涤剂不会导致水体污染,是因为其易被细菌分解
D.太阳能电池板中的硅在元素周期表中处于金属与非金属的交界位置
1.建筑一个容积为8000 m3,深为6 m的长方体蓄水池,池壁的造价为a元/m2,池底的造价为2a元/m2,把总造价y(元)表示为底的一边长为x(m)的函数.
解:设底面的另一边长为z(m),则根据题意有6xz=8000,z=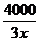
池壁造价为a·(2x+2z)·6=12a(x+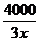 )
)
池底造价为2a·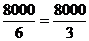 a
a
所以,总造价:y=[12a(x+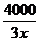 )+
)+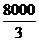 a](元)
a](元)
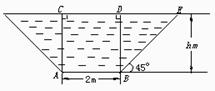 2.如图,灌溉渠的横截面是等腰梯形,底宽2 m,边坡的倾角为45°,水深h m,求横断面中有水面积A(m2)与水深h(m)的函数关系式
2.如图,灌溉渠的横截面是等腰梯形,底宽2 m,边坡的倾角为45°,水深h m,求横断面中有水面积A(m2)与水深h(m)的函数关系式
解:如图,作AC⊥CE,BD⊥CE,
∴Rt△BDE面积: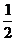 h
h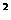 ,矩形面积:2h
,矩形面积:2h
∴A=S矩+2 =2h+2×
=2h+2×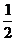 h
h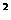 =h
=h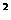 +2h(m
+2h(m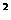 )
)
2.如图,有一块边长为a的正方形铁皮,将其四个角各截去一个边长为x的小正方形,然后折成一个无盖的盒子,写出体积V以x为自变量的函数式,并讨论这个函数的定义域.
解:∵底面边长为a-2x,∴底面积为(a-2x)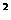
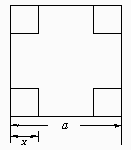
又长方体高为x,∴长方体体积V=x(a-2x)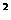
由a-2x>0,得x<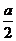
又x>0,∴函数定义域为{x|0<x<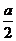
课本P89习题2.9
课本P88练习
1.将一个底面圆的直径为d的圆柱截成横截面为长方形的棱柱,若这个长方形截面的一条边长为x,对角线长为d,截面的面积为A,求面积A以x为自变量的函数式,并写出它的定义域.
解:如图,截面的一条边为x,对角线AC=d,另一条边BC=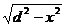 ,所以S=x
,所以S=x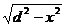 ,定义域为:{x|0<x<d
,定义域为:{x|0<x<d
2.销售额问题
某县乡镇企业局,要求预测1990年-1991年轻工产品人均销售额,根据初步分析,人均销售额yt和人均国民收人xt的数据如下表所示,1990年及1991年人均国民收入计划值分别为514.1元/人、 550.l元/人.
|
年份 |
人均销售额yt(元/人) |
人均国民收入xt(元/人) |
年份 |
人均销售额yt(元/人) |
人均国民收入xt(元/人) |
|
1965 |
0.35 |
116 |
1978 |
0.78 |
197 |
|
1966 |
0.37 |
137 |
1979 |
0.94 |
226 |
|
1967 |
0.52 |
142 |
1980 |
1.00 |
238 |
|
1968 |
0.67 |
156 |
1981 |
1.05 |
258 |
|
1969 |
0.60 |
123 |
1982 |
1.10 |
254 |
|
1970 |
0.57 |
115 |
1983 |
1.18 |
269 |
|
1970 |
0.53 |
128 |
1984 |
1.22 |
270 |
|
1972 |
0.59 |
136 |
1985 |
1.36 |
188 |
|
1973 |
0.50 |
162 |
1986 |
1.45 |
348 |
|
1974 |
0.56 |
186 |
1987 |
1.61 |
422 |
|
1975 |
0.63 |
162 |
1988 |
1.86 |
448 |
|
1976 |
0.66 |
163 |
1989 |
2.11 |
485 |
|
1977 |
0.77 |
173 |
|
|
|
1.中国人口问题
“人口问题”是我国最大的社会问题之一,估计人口数量和发展趋势是我们制定一系列相关政策的基础.由人口统计年鉴,可查得我国从1949年到1994年人口数据资料如下:
|
年 |
1949 |
1954 |
1959 |
1964 |
1969 |
1974 |
1979 |
1989 |
1994 |
|
人口(百万) |
541.67 |
602.66 |
672.09 |
704.99 |
806.71 |
908.59 |
975.42 |
1106.76 |
1176.74 |
试估计我国2010年的人口数.
数学模型与数学建模
数学模型就是把实际问题用数学语言抽象概括,再从数学角度来反映或近似地反映实际问题时,所得出的关于实际问题的数学描述.
数学模型方法,是把实际问题加以抽象概括,建立相应的数学模型,利用这些模型来研究实际问题的一般数学方法.
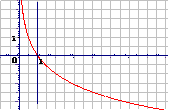
3.对数函数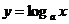
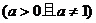 的图像和性质:
的图像和性质:
|
|
a>1 |
0<a<1 |
|
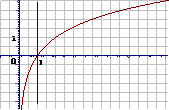
图 象 |
 |
 |
|
性 质 |
定义域:(0,+∞) |
|
|
值域:R |
||
过点(1,0),即当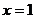 时, 时,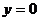 |
||
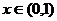 时 时 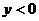  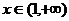 时 时 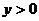  |
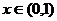 时 时  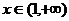 时 时 |
|
在(0,+∞)上是增函数 |
在(0,+∞)上是减函数 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com