2．　 抓住几个点

(1)　　 伸到最长的点，压缩到最短的点

(2)　　 弹簧原长的点

(3)　　 受力平衡的点

弹簧长度的变化影响力的变化，因此研究时往往比较复杂

1．　 一般弹簧弹力不会随外力变化而突变，但如果事情值弹簧，一端没有束缚的情况下弹力也会突变

　例：竖直光滑杆上套有一个小球和两根弹簧，两弹簧的一端各与小球相连，另一端分别用销钉M、N固定与杆上，小球处于静止状态，设拔去销钉M瞬间，小球的加速度大小为12m/s²，若不拔去销钉M而拔去销钉N瞬间，小球的加速度可能是多少？(g = 10m/s)

分析：拔去销钉瞬间，小球加速度的大小为12m/s²，方向可以向上也可以向下

当a向上时：N – G = ma　 上部弹簧的力为ma　 方向向下　　　　　

撤掉N　 ma + mg = ma₁ a₁ = 22m/s²

当a向下时：N + G = ma　 上部弹簧的力为ma　 方向向上

撤掉N　 ma – mg = ma₁　　 　a₁ = 2m/s²

2．失重：视重< 实重　 a竖直向下　　 G-N = ma

　　　　 加速下降或减速上升

　　 例：(1994年上海)原来作匀速运动的升降机内，有一被伸长弹簧拉住的，具有一定质量的物体A静止在地板上，如图，现发现A突然被弹簧拉向右方，由此可判断，此升降机的运动可能是：B

A．　 加速上升

B． 减速上升

C．　　 下降

D．　　 减速下降

1．超重：视重 >实重　 a竖直向上　　 N-G = ma

　　　　 加速上升或减速下降

5．　 矢量法 :

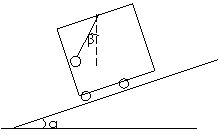例：如图，倾角为α的斜坡上行驶着一辆小车，车顶吊着一只单摆，一观察者测得摆线与竖直方向的夹角为β，则可判断小车的加速度大小为：B

A．a = gsinβ/ sin(α+β)

B．a = gsinβ/ cos(α+β)

C．a = gsinβ/ sinα

D．a = gsinα

分析：小球受到重力、拉力与合力组成矢量三角形

mg/ sin(90°-α-β) = ma/sinβ

α= gsinβ/cos(α+β)

4．　 系统牛顿第二定律

对连接体，可以在几个物体加速度不同时，考虑合力与加速度的关系

∑F = m₁a₁+m₂a₂+ …

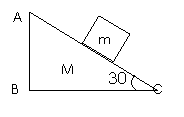例3(1994年全国)质量M=10千克的木楔ABC静置于粗糙水平面上，滑动摩擦系数μ=0.02，在木楔的倾角为30º的斜面上，有一质量m=1.0千克的物块由静止开始沿斜面下滑，如图，当滑行路程s=1.4m时，其速度v=1.4m/s，在这过程中木楔没有动，，求地面对木楔的摩擦力的大小和方向。(g=10m/s)

分析：物块滑下　 2as = v²　　　 a = 0.7m/s²

a_∥=acosθ=0.61m/s²

f = ma_∥=1.0kg×a_∥=0.61N　　 水平向右

3．　 分解加速度

解决动力学问题分解方法有两种，一种是分解力，一种是分解加速度

例：自动扶梯与地面夹角为30º，当

扶梯沿斜面向上作匀加速运动时，

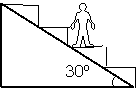人对梯面的压力是其重力的6/5，则

人与梯面的摩擦力是其重力的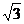：(/5)

2．　　 整体法与隔离法的应用

①　　 隔离法分析内力

例2．(1993年上海)如图所示，木块A与B用一轻弹簧相连，竖直放在木块C上，三者都置于地面，它们的质量之比是1∶2∶3，所有接触面都光滑，当沿水平方向迅速抽出木块C的瞬间，

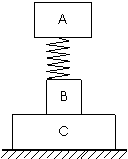A和B的加速度分别是 ,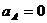 　　　　

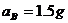
分析：三木块在地面上静止时，木块A受到向下重力和向上的弹力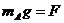，木块B受到向下的重力和向下的弹力向上的支持力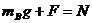，抽出C后弹力不会立即变化∴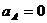

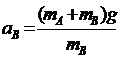
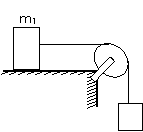
②　　 整体法分析系统加速度

　　　　 在解决连接题问题时，往往先用整体

　　　　　 例3．如图，m₂拉m₁向下做加速运动，m₁与桌面摩擦系数为μ，求加速度

　　　　　　　　 a = ( m₂g -μm₁g)/(m₁+m₂)

③　　 　综合应用--先整体后分离

例4．如图质量为2m的物块A与水平地面的摩擦可忽略不计，质量为m的物块B与地面的摩擦系数为μ，在已知水平推力F的作用下，A、B作加速运动，则A对B的作用力为　　 　　　　

分析：整体：　 F – μmg = 3ma　

　 a = ( F – μmg ) / 3m

对B：　 N – μmg = ma　　

　 N = F/3 +2μmg/3

　 例5．(1990上海)如图所示，三个物体质量分别为m₁、m₂和m₃，带有滑轮的物体放在光滑水平面上，滑轮和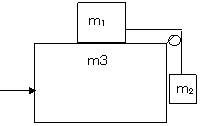所有接触面的摩擦及绳子的质量均不计，为使三个物体无相对运动，水平推力F等于　　　　　　　　 。

　　　　　 F = (m₁+m₂+m₃)a　　　　 m₁：T = m₁a

　　　　　 m₂：竖直方向没有加速度， m₂g = T　

　　　　　 F = (m₁+m₂+m₃)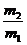g

1．正交分解法

物体做加速运动：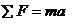

取两相互垂直的方向，正交表示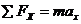　 　　

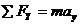
例：在水平地面上有一质量为5千克的物体，在与水平方向成53°沿斜上方的25牛顿拉力时，恰好做匀速直线运动　　　　　　　　　　　　　　　　　

(1)　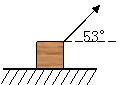　 当拉力为50牛时，加速度多大？

(2)　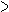　 当拉力为62.5牛时，加速度多大？

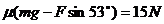
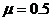
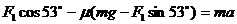
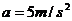
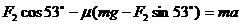
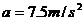
3.　　 牛顿定三定律:

物体间的作用总是相互的,“两个物体之间的作用力和反作用力总是大小相等,方向相反,作用在一条直线上”。

注意：(1)相互作用力与平衡力的区别。

(3)　　 相互作用力与物体所处的状态无关。