
2、过程与方法
(1)通过已学过的函数特别是二次函数,理解函数的单调性及其几何意义;
(2)学会运用函数图象理解和研究函数的性质;
(3)能够熟练应用定义判断与证明函数在某区间上的单调性.
1、知识与技能:
(1)建立增(减)函数的概念
通过观察一些函数图象的特征,形成增(减)函数的直观认识. 再通过具体函
数值的大小比较,认识函数值随自变量的增大(减小)的规律,由此得出增(减)函数单调性的定义 . 掌握用定义证明函数单调性的步骤。
(2)函数单调性的研究经历了从直观到抽象,以图识数的过程,在这个过程中,让学生通过自主探究活动,体验数学概念的形成过程的真谛。
(六)设置问题,留下悬念.
1.课本P45(A组) 6.7.8
2.求函数 的最小值.
的最小值.
3.求函数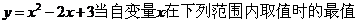 .
.
①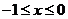 ②
② 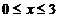 ③
③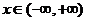
§1.3.1函数的单调性
(五)归纳小结
求函数最值的常用方法有:
(1)配方法:即将函数解析式化成含有自变量的平方式与常数的和,然后根据变量的取值范围确定函数的最值.
(2)换元法:通过变量式代换转化为求二次函数在某区间上的最值.
(3)数形结合法:利用函数图象或几何方法求出最值.
(四)巩固深化,反馈矫正.
(1)P38练习4
(2)求函数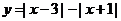 的最大值和最小值.
的最大值和最小值.
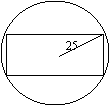
(3)如图,把截面半径为25cm的图形木头锯成矩形木料,如果矩形一边长为 ,面积为
,面积为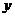 ,试将
,试将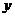 表示成
表示成 的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?
的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?
(三)质疑答辩,排难解惑.
例1.(教材P36例3)利用二次函数的性质确定函数的最大(小)值.
解(略)
例2.将进货单价40元的商品按50元一个售出时,能卖出500个,若此商品每个涨价1元,其销售量减少10个,为了赚到最大利润,售价应定为多少?
解:设利润为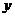 元,每个售价为
元,每个售价为 元,则每个涨(
元,则每个涨( -50)元,从而销售量减少
-50)元,从而销售量减少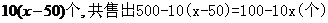
∴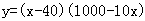
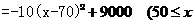 <100)
<100)
∴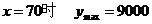
答:为了赚取最大利润,售价应定为70元.
例3.求函数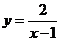 在区间[2,6]
上的最大值和最小值.
在区间[2,6]
上的最大值和最小值.
解:(略)
例4.求函数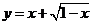 的最大值.
的最大值.
解:令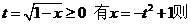
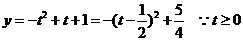
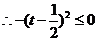
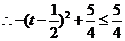

(二)研探新知
1.函数最大(小)值定义
最大值:一般地,设函数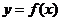 的定义域为I,如果存在实数M满足:
的定义域为I,如果存在实数M满足:
(1)对于任意的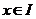 ,都有
,都有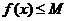 ;
;
(2)存在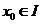 ,使得
,使得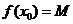 .
.
那么,称M是函数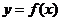 的最大值.
的最大值.
思考:依照函数最大值的定义,结出函数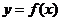 的最小值的定义.
的最小值的定义.
注意:
①函数最大(小)首先应该是某一个函数值,即存在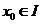 ,使得
,使得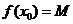 ;
;
②函数最大(小)应该是所有函数值中最大(小)的,即对于任意的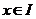 ,都有
,都有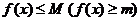 .
.
2.利用函数单调性来判断函数最大(小)值的方法.
①配方法 ②换元法 ③数形结合法
(一)创设情景,揭示课题.
画出下列函数的图象,指出图象的最高点或最低点,并说明它能体现函数的什么特征?
①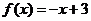 ②
②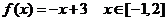
③ ④
④
2.教学用具:多媒体手段
1.学法:学生通过画图、观察、思考、讨论,从而归纳出求函数的最大(小)值的方法和步骤.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com