
学法:通过图象,理解对数函数与指数函数的关系.
教具:多媒体
重点:指数函数与对数函数内在联系
难点:反函数概念的理解
3. 情感、态度、价值观
(1)体会指数函数与指数;
(2)进一步领悟数形结合的思想.
2.过程与方法
学生通过观察和类比函数图象,体会两种函数的单调性差异.
1.知识与技能
(1)知识与技能
(2)了解反函数的概念,加深对函数思想的理解.
4.已知0< <1, b>1,
ab>1. 比较
<1, b>1,
ab>1. 比较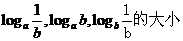
归纳小结:
② 对数函数的概念必要性与重要性;
②对数函数的性质,列表展现.
对数函数(第三课时)
3.已知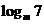 <
<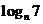 <0,按大小顺序排列m, n, 0, 1
<0,按大小顺序排列m, n, 0, 1
2.求函数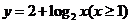 的值域.
的值域.
1.已知函数 的定义域为[-1,1],则函数
的定义域为[-1,1],则函数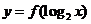 的定义域为
的定义域为
1. 比较下列各组数中的两个值大小
(1)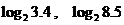
(2)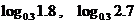
(3)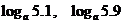 (
( >0,且
>0,且 ≠1)
≠1)
分析:由数形结合的方法或利用函数的单调性来完成:
(1)解法1:用图形计算器或多媒体画出对数函数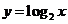 的图象.在图象上,横坐标为3、4的点在横坐标为8.5的点的下方:
的图象.在图象上,横坐标为3、4的点在横坐标为8.5的点的下方:
所以,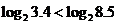
解法2:由函数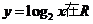 +上是单调增函数,且3.4<8.5,所以
+上是单调增函数,且3.4<8.5,所以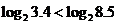 .
.
解法3:直接用计算器计算得: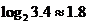 ,
,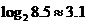
(2)第(2)小题类似
(3)注:底数是常数,但要分类讨论 的范围,再由函数单调性判断大小.
的范围,再由函数单调性判断大小.
解法1:当 >1时,
>1时,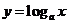 在(0,+∞)上是增函数,且5.1<5.9.
在(0,+∞)上是增函数,且5.1<5.9.
所以,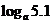
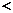
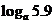
当
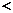 1时,
1时,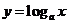 在(0,+∞)上是减函数,且5.1<5.9.
在(0,+∞)上是减函数,且5.1<5.9.
所以,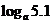
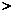
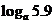
解法2:转化为指数函数,再由指数函数的单调判断大小不一,
令 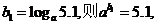 令
令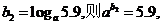 则
则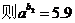
当 >1时,
>1时,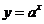 在R上是增函数,且5.1<5.9
在R上是增函数,且5.1<5.9
所以,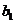 <
<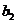 ,即
,即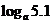 <
<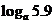
当0< <1时,
<1时,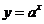 在R上是减函数,且5.1>5.9
在R上是减函数,且5.1>5.9
所以,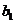 <
<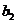 ,即
,即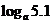 >
>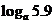
说明:先画图象,由数形结合方法解答
课堂练习:P85 练习 第2,3题
补充练习
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com