
6.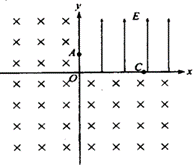 (07·全国理综Ⅱ·25) 如图所示,在坐标系Oxy的第一象限中存在沿y轴正方向的匀速磁场,场强大小为E。在其它象限中存在匀强磁场,磁场方向垂直于纸面向里。A是y轴上的一点,它到坐标原点O的距离为h;C是x轴上的一点,到O的距离为L。一质量为m,电荷量为q的带负电的粒子以某一初速度沿x轴方向从A点进入电场区域,继而通过C点进入磁场区域。并再次通过A点,此时速度方向与y轴正方向成锐角。不计重力作用。试求:
(07·全国理综Ⅱ·25) 如图所示,在坐标系Oxy的第一象限中存在沿y轴正方向的匀速磁场,场强大小为E。在其它象限中存在匀强磁场,磁场方向垂直于纸面向里。A是y轴上的一点,它到坐标原点O的距离为h;C是x轴上的一点,到O的距离为L。一质量为m,电荷量为q的带负电的粒子以某一初速度沿x轴方向从A点进入电场区域,继而通过C点进入磁场区域。并再次通过A点,此时速度方向与y轴正方向成锐角。不计重力作用。试求:
⑴粒子经过C点速度的大小和方向;
⑵磁感应强度的大小B。
解:⑴以a表示粒子在电场作用下的加速度,有qE=ma ①
加速度沿y轴负方向。设粒子从A点进入电场时的初速度为v0,由A点运动到C点经历的时间为t,则有
 h=
h=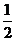 at2 ②
at2 ②
l=v0t ③
由②③式得: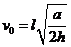 ④
④
设粒子从C点进入磁场时的速度为v,v垂直于x轴的分量
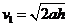 ⑤
⑤
由①④⑤式得: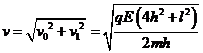 ⑥
⑥
设粒子经过C点时的速度方向与x轴的夹角为α,则有
tanα=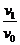 ⑦
⑦
由④⑤⑦式得:α=arctan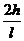 ⑧
⑧
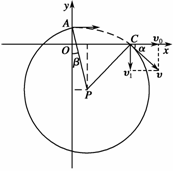
⑵粒子经过C点进入磁场后在磁场中作速率为v的圆周运动。若圆周的半径为R,则有:
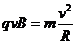 ⑨
⑨
设圆心为P,则PC必与过C点的速度垂直,且有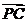 =
= =R。用β表示
=R。用β表示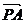 与y轴的夹角,由几何关系得
与y轴的夹角,由几何关系得
Rcosβ=Rcosα+h ⑩
Rsinβ=l-Rsinα

由⑧⑩ 式解得:
式解得:
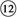
由⑥⑨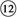 式解得:
式解得:

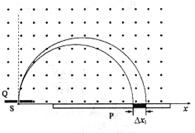
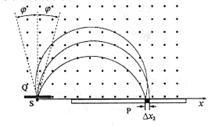
5. (07·江苏·17)磁谱仪是测量α能谱的重要仪器。磁谱仪的工作原理如图所示,放射源S发出质量为m、电量为q的α粒子沿垂直磁场方向进入磁感应强度为B的匀强磁场,被限束光栏Q限制在2φ的小角度内,α粒子经磁场偏转后打到与束光栏平行的感光片P上。(重力影响不计)
(07·江苏·17)磁谱仪是测量α能谱的重要仪器。磁谱仪的工作原理如图所示,放射源S发出质量为m、电量为q的α粒子沿垂直磁场方向进入磁感应强度为B的匀强磁场,被限束光栏Q限制在2φ的小角度内,α粒子经磁场偏转后打到与束光栏平行的感光片P上。(重力影响不计)
⑴若能量在E-E+ΔE(ΔE>0,且
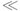 E)范围内的α粒子均垂直于限束光栏的方向进入磁场。试求这些α粒子打在胶片上的范围Δx1。
E)范围内的α粒子均垂直于限束光栏的方向进入磁场。试求这些α粒子打在胶片上的范围Δx1。
⑵实际上,限束光栏有一定的宽度,α粒子将在2φ角内进入磁场。试求能量均为E的α 粒子打到感光胶片上的范围Δx2
解:(1)设α粒子以速度v进入磁场,打在胶片上的位置距S的距离为x
 圆周运动
圆周运动 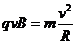
α粒子的动能 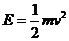
且 x=2R
解得: 
 由上式可得:
由上式可得: 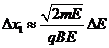
(2)动能为E的α粒子沿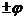 角入射,轨道半径相同,设为R
角入射,轨道半径相同,设为R
圆周运动 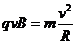
α粒子的动能 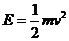
由几何关系得 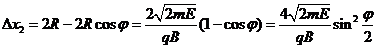
4.(07·广东物理·20)如图为装置的垂直截面图,虚线A1A2是垂直截面与磁场区边界面的交线,匀
强磁场分布在A1A2的右侧区域,磁感应强度B=0.4T,方向垂直纸面向外,A1A2与垂直截面上的水平线夹角为45°。在A1A2左侧,固定的薄板和等大的挡板均水平放置,它们与垂直截面交线分别为S1、S2,相距L=0.2 m。在薄板上P处开一小孔,P与A1A2线上点D的水平距离为L。在小孔处装一个电子快门。起初快门开启,一旦有带正电微粒通过小孔,快门立即关闭,此后每隔T=3.0×10-3 s开启一次并瞬间关闭。从S1S2之间的某一位置水平发射一速度为v0的带正电微粒,它经过磁场区域后入射到P处小孔。通过小孔的微粒与档板发生碰撞而反弹,反弹速度大小是碰前的0.5倍。
(1)过一次反弹直接从小孔射出的微粒,其初速度v0应为多少?
⑵求上述微粒从最初水平射入磁场到第二次离开磁场的时间。(忽略微粒所受重力影响,碰撞过程无电荷转移。已知微粒的荷质比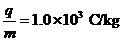 。只考虑纸面上带电微粒的运动)
。只考虑纸面上带电微粒的运动)
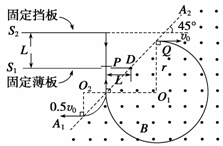 解:⑴如图所示,设带正电微粒在S1S2之间任意点Q以水平速度v0进入磁场,微粒受到的洛仑兹力为f,在磁场中做圆周运动的半径为r,有:
解:⑴如图所示,设带正电微粒在S1S2之间任意点Q以水平速度v0进入磁场,微粒受到的洛仑兹力为f,在磁场中做圆周运动的半径为r,有:
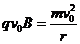
解得:
欲使微粒能进入小孔,半径r的取值范围为: 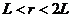
代入数据得:80 m/s<v0<160 m/s
欲使进入小孔的微粒与挡板一次相碰返回后能通过小孔,还必须满足条件:
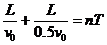 其中n=1,2,3,……
其中n=1,2,3,……
可知,只有n=2满足条件,即有:v0=100 m/s
⑵设微粒在磁场中做圆周运动的周期为T0,从水平进入磁场到第二次离开磁场的总时间为t,设t1、t4分别为带电微粒第一次、第二次在磁场中运动的时间,第一次离开磁场运动到挡板的时间为t2,碰撞后再返回磁场的时间为t3,运动轨迹如答图所示,则有:
 ;
; 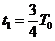 ;
; 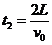 ;
; 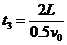 ;
; 
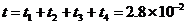 s
s
3.(07·广东物理·19)如图所示,沿水平方向放置一条平直光滑槽,它垂直穿过开有小孔的两平行薄板,板相距3.5L。槽内有两个质量均为m的小球A和B,球A带电量为 +2q,球B带电量为-3q,两球由长为2L的轻杆相连,组成一带电系统。最初A和B分别静止于左板的两侧,离板的距离均为L。若视小球为质点,不计轻杆的质量,在两板间加上与槽平行向右的匀强电场E后(设槽和轻杆由特殊绝缘材料制成,不影响电场
的分布),求:
⑴球B刚进入电场时,带电系统的速度大小;
⑵带电系统从开始运动到速度第一次为零所需的时间及球A相对右板的位置。
答案 对带电系统进行分析,假设球A能达到右极板,电场力对系统做功为W1,有:
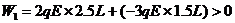 由此可以判定,球A不仅能达到右极板,
由此可以判定,球A不仅能达到右极板,
而且还能穿过小孔,离开右极板。假设球B能达到右极板,电场力对系统做功为W2,有: 由此判定,球B不能达到右极板
由此判定,球B不能达到右极板
综上所述,带电系统速度第一次为零时,球A、B应分别在右极板两侧。
(1)电系统开始运动时,设加速度为a1,由牛顿第二定律: =
=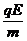
球B刚进入电场时,带电系统的速度为v1,有: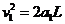
求得: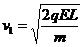
⑵设球B从静止到刚进入电场的时间为t1,则: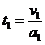
解得: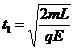
球B进入电场后,带电系统的加速度为a2,由牛顿第二定律: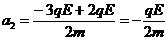
显然,带电系统做匀减速运动。设球A刚达到右极板时的速度为v2,减速所需时间为t2,则有: 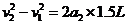
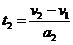
求得: 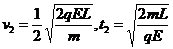
球A离电场后,带电系统继续做减速运动,设加速度为a3,再由牛顿第二定律:
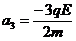
设球A从离开电场到静止所需的时间为t3,运动的位移为x,则有: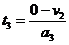
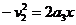
求得: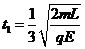
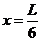
可知,带电系统从静止到速度第一次为零所需的时间为:
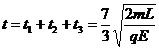
 球A相对右板的位置为:
球A相对右板的位置为: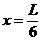
2.(05.广东物理·8)关于电磁场和电磁波,下列说法正确的是 ( ACD )
A.电磁波是横波
B.电磁波的传播需要介质
C.电磁波能产生干涉和衍射现象
D.电磁波中电场和磁场方向处处互相垂直
1.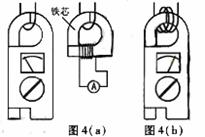 (05.广东物理·9)钳形电流表的结构如图4(a)所示。图4(a)中电流表的读数为1.2A。图4(b)中用同一电缆线绕了3匝,则
( C
)
(05.广东物理·9)钳形电流表的结构如图4(a)所示。图4(a)中电流表的读数为1.2A。图4(b)中用同一电缆线绕了3匝,则
( C
)
A.这种电流表能测直流电流,图4(b)的读数为2.4A
B.这种电流表能测交流电流,图4(b)的读数为0.4A
C.这种电流表能测交流电流,图4(b)的读数为3.6A
D.这种电流表既能测直流电流,又能测交流电流,图4(b)的读数为3.6A
7.(08上海物理·20 B)某小型实验水电站输出功率是20kW,输电线路总电阻是6Ω。
(1)若采用380 V输电,求输电线路损耗的功率。
(2)若改用5000 V高压输电,用户端利用n1:n2=22:1的变压器降压,求用户得到的电压。
答案:见解析
解析:(1)输电线上的电流强度为I=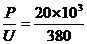 A=52.63A
A=52.63A
输电线路损耗的功率为P损=I2R=52.632×6W≈16620W=16.62kW
(2)改用高压输电后,输电线上的电流强度变为I′=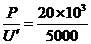 A=4A
A=4A
用户端在变压器降压前获得的电压 U1=U-I′R=(5000-4×6)V=4976V
根据 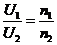
用户得到的电压为U2=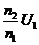 =
=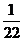 ×4976V=226.18V
×4976V=226.18V
题组二
6.(08·广东·5)小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间呈正弦函数关系,如图所示国。此线圈与一个R=10Ω的电阻构成闭合电路,不计电路的其他电阻。下列说法正确的是 ( C )
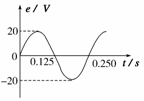 A.交变电流的周期为0.125s
A.交变电流的周期为0.125s
B.交变电流的频率为8Hz
C.交变电流的有效值为 A
A
D.交变电流的最大值为4A
[解析]由e-t图像可知,交变电流电流的周期为0.25s,故频率为4Hz,选项A、B错误。根据欧姆定律可知交变电流的最大值为2A,故有效值为 A,选项C正确。
A,选项C正确。
5.(08·海南·7)如图,理想变压器原副线圈匝数之比为4∶1.原线圈接入一电压为u=U0sinωt的交流电源,副线圈接一个R=27.5 Ω的负载电阻.若U0=220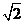 V,ω=100π Hz,则下述结论正确的是 ( AC )
V,ω=100π Hz,则下述结论正确的是 ( AC )
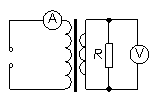 A.副线圈中电压表的读数为55 V
A.副线圈中电压表的读数为55 V
B.副线圈中输出交流电的周期为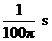
C.原线圈中电流表的读数为0.5 A
D.原线圈中的输入功率为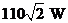
[解析]:原线圈电压有效值U1=220V,由电压比等于匝数比可得副线圈电压U2=55V,A对;电阻R上的电流为2A,由原副线圈电流比等于匝数的反比,可得电流表示数为0.5A, C对;输入功率为P=220×0.5W=110W,D错;周期T= =0.02s,B错。
4.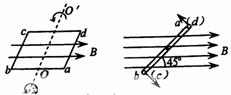 (08宁夏·19)如图a所示,一矩形线圈abcd放置在匀强磁场中,并绕过ab、cd中点的轴OO′以角速度
(08宁夏·19)如图a所示,一矩形线圈abcd放置在匀强磁场中,并绕过ab、cd中点的轴OO′以角速度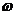 逆时针匀速转动。若以线圈平面与磁场夹角
逆时针匀速转动。若以线圈平面与磁场夹角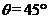 时(如图b)为计时起点,并规定当电流自a流向b时电流方向为正。则下列四幅图中正确的是
时(如图b)为计时起点,并规定当电流自a流向b时电流方向为正。则下列四幅图中正确的是 ( D )
( D )
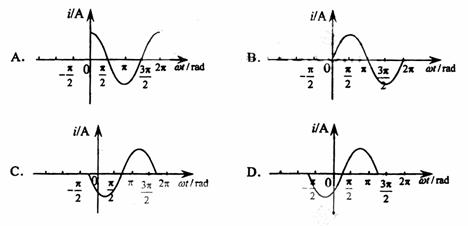
[解析]本题考查正弦交流电的产生过程、楞次定律等知识和规律。从a图可看出线圈从垂直于中性面开始旋转,由楞次定律可判断,初始时刻电流方向为b到a,故瞬时电流的表达式为i=-imcos(+ωt),则图像为D图像所描述。平时注意线圈绕垂直于磁场的轴旋转时的瞬时电动势表达式的理解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com