
53.(07宁夏理综 )如图所示,两个可导热的气缸竖直放置,它们的底部都由一细管连通(忽略细管的容积)。两气缸各有一个活塞,质量分别为m1和m2,活塞与气缸无摩擦。活塞的下方为理想气体,上方为真空。当气体处于平衡状态时,两活塞位于同一高度h。(已知m1=3m,m2=2m)
⑴在两活塞上同时各放一质量为m的物块,求气体再次达到平衡后两活塞的高度差(假定环境温度始终保持为T0)。
⑵在达到上一问的终态后,环境温度由T0缓慢上升到T,试问在这个过程中,气体对活塞做了多少功?气体是吸收还是放出了热量?(假定在气体状态变化过程中,两物块均不会碰到气缸顶部)。
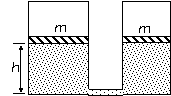
解析:⑴设左、右活塞的面积分别为A/和A,由于气体处于平衡状态,故两活塞对气体的压强相等,即:

由此得: 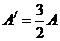
在两个活塞上各加一质量为m的物块后,右活塞降至气缸底部,所有气体都在左气缸中。
在初态,气体的压强为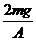 ,体积为
,体积为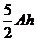 ;在末态,气体压强为
;在末态,气体压强为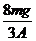 ,体积为
,体积为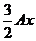 (x为左活塞的高度)。由玻意耳-马略特定律得:
(x为左活塞的高度)。由玻意耳-马略特定律得:

解得: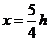 即两活塞的高度差为
即两活塞的高度差为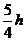
⑵当温度由T0上升至T时,气体的压强始终为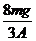 ,设x/是温度达到T时左活塞的高度,由盖·吕萨克定律得:
,设x/是温度达到T时左活塞的高度,由盖·吕萨克定律得: 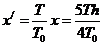
活塞对气体做的功为: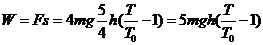
在此过程中气体吸收热量
52.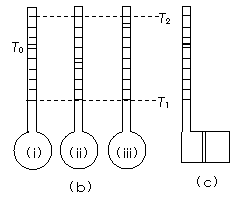
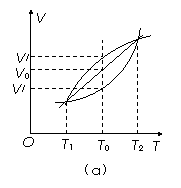 (07上海卷)一定量的理想气体与两种实际气体I、II在标准大气压下做等压变化时的V-T关系如图(a)所示,图中=。用三份上述理想气体作为测温物质制成三个相同的温度计,然后将其中二个温度计中的理想气体分别换成上述实际气体I、II。在标准大气压下,当环境温度为T0时,三个温度计的示数各不相同,如图(b)所示,温度计(ii)中的测温物质应为实际气体________(图中活塞质量忽略不计);若此时温度计(ii)和(iii)的示数分别为21°C和24°C,则此时温度计(i)的示数为________°C;可见用实际气体作为测温物质时,会产生误差。为减小在T1-T2范围内的测量误差,现针对T0进行修正,制成如图(c)所示的复合气体温度计,图中无摩擦导热活塞将容器分成两部分,在温度为T1时分别装入适量气体I和II,则两种气体体积之比VI:VII应为________。
(07上海卷)一定量的理想气体与两种实际气体I、II在标准大气压下做等压变化时的V-T关系如图(a)所示,图中=。用三份上述理想气体作为测温物质制成三个相同的温度计,然后将其中二个温度计中的理想气体分别换成上述实际气体I、II。在标准大气压下,当环境温度为T0时,三个温度计的示数各不相同,如图(b)所示,温度计(ii)中的测温物质应为实际气体________(图中活塞质量忽略不计);若此时温度计(ii)和(iii)的示数分别为21°C和24°C,则此时温度计(i)的示数为________°C;可见用实际气体作为测温物质时,会产生误差。为减小在T1-T2范围内的测量误差,现针对T0进行修正,制成如图(c)所示的复合气体温度计,图中无摩擦导热活塞将容器分成两部分,在温度为T1时分别装入适量气体I和II,则两种气体体积之比VI:VII应为________。
答案:II; 23; 2:1
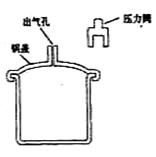
51.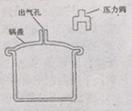 (07年山东卷)某压力锅结构如图所示。盖好密封锅盖,将压力阀套在出气孔上,给压力锅加热,当锅内气体压强达到一定值时,气体就把压力阀顶起。假定在压力阀被顶起时,停止加热。
(07年山东卷)某压力锅结构如图所示。盖好密封锅盖,将压力阀套在出气孔上,给压力锅加热,当锅内气体压强达到一定值时,气体就把压力阀顶起。假定在压力阀被顶起时,停止加热。
(1)若此时锅内气体的体积为V,摩尔体积为V0,阿伏加德罗常数为NA,写出锅内气体分子数的估算表达式。
(2)假定在一次放气过程中,锅内气体对压力阀及外界做功1J,并向外界释放了2J的热量。锅内原有气体的内能如何变化?变化了多少?
(3)已知大气压强P随海拔高度H的变化满足P=P0(1-αH),其中常数α>0。结合
气体定律定性分析在不同的海拔高度使用压力锅,当压力阀被顶起时锅内气体的温度
有何不同。
解析:(1)设锅内气体分子数为n
n=V/V0·NA
(2)根据热力学第一定律
ΔE=W+Q=-3J
锅内气体内能减少,减少了3J
(3)由P=P0(1-αH)(其中α>0)知,随着海拔高度的增加,大气压强减小;
由P1=P+mg/S知,随着海拔高度的增加,阀门被顶起时锅内气体压强减小;
根据查理定律P1/T1=P2/T2
可知阀门被顶起时锅内气体温度随着海拔高度的增加而低。
50.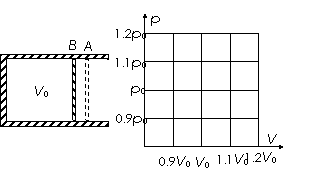 (07上海卷)如图所示,水平放置的汽缸
(07上海卷)如图所示,水平放置的汽缸
内壁光滑,活塞厚度不计,在A、B两处设
有限制装置,使活塞只能在A、B之间运
动,B左面汽缸的容积为V0,A、B之间
的容积为0.1V0。开始时活塞在B处,缸
内气体的压强为0.9p0(p0为大气压强),温度
为297 K,现缓慢加热汽缸内气体,直至399.3 K。求:
⑴活塞刚离开B处时的温度TB;
⑵缸内气体最后的压强p;
⑶在右图中画出整个过程的p-V图线。
解析:⑴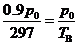 解得:TB=333 K
解得:TB=333 K
⑵ 解得:p=1.1p0,
解得:p=1.1p0,
⑶图略。
49.(07上海理科综合)潮汐能属于无污染能源,但能量的转化率较低,相比之下,核能是一种高效的能源。
⑴在核电站中,为了防止放射性物质泄漏,核反应堆有三道防护屏障:燃料包壳,压力壳和安全壳(见图1)。结合图2可知,安全壳应当选用的材料是 。
⑵核反应堆中的核废料具有很强的放射性,目前常用的处理方法是将其装入特制的容器中,然后
A.沉入海底 B.放至沙漠 C.运到月球 D.深埋地下
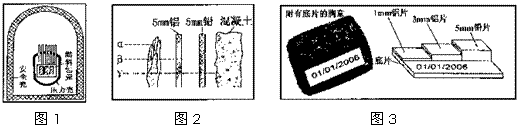
⑶图3是用来监测工作人员受到辐射情况的胸章,通过照相底片被射线感光的区域,可以判断工作人员受到何种辐射。当胸章上1 mm铝片和3 mm铝片下的照相底片被感光,而铅片下的照相底片未被感光时,结合图2分析工作人员受到了 射线的辐射;当所有照相底片被感光时,工作人员受到了 射线的辐射。
答案:⑴混凝土 ⑵D ⑶β;γ或“β和γ”
48.(07山东理综)某压力锅结构如图所示。盖好密封锅盖,将压力阀套在出气孔上,给压力锅加热,当锅内气体压强达到一定值时,气体就把压力阀顶起。假定在压力阀被顶起时,停止加热。
 ⑴若此时锅内气体的体积为V,摩尔体积为V0,阿伏加
⑴若此时锅内气体的体积为V,摩尔体积为V0,阿伏加
德罗常数为NA,写出锅内气体分子数的估算表达式。
⑵假定在一次放气过程中,锅内气体对压力阀及外界做
功1 J,并向外界释放了2 J的热量。锅内原有气体的内能如
何变化?变化了多少?
⑶已知大气压强P随海拔高度H的变化满足
P=P0(1-αH),其中常数α>0。结合气体定律定性分析在不同的海拔高度使用压力锅,当压力阀被顶起时锅内气体的温度有何不同。
解析:⑴设锅内气体分子数为n
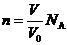
⑵根据热力学第一定律得:ΔU=W+Q=-3 J
锅内气体内能减少,减少了3 J
⑶由P=P0(1-αH)(其中α>0)知,随着海拔高度的增加,大气压强减小。
由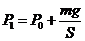 知,随着海拔高度的增加,阀门被顶起时锅内气体压强减小。
知,随着海拔高度的增加,阀门被顶起时锅内气体压强减小。
根据查理定律得: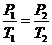
可知阀门被顶起时锅内气体温度随着海拔高度的增加而降低。
47. (07上海卷)如图所示,水平放置的汽缸内壁光滑,活塞厚度不计,在A、B两处设有限制装置,使活塞只能在A、B之间运动,B左面汽缸的容积为V0,A、B之间的容积为0.1V0。开始时活塞在B处,缸内气体的压强为0.9p0(p0为大气压强),温度为297K,现缓慢加热汽缸内气体,直至399.3K。求:
(07上海卷)如图所示,水平放置的汽缸内壁光滑,活塞厚度不计,在A、B两处设有限制装置,使活塞只能在A、B之间运动,B左面汽缸的容积为V0,A、B之间的容积为0.1V0。开始时活塞在B处,缸内气体的压强为0.9p0(p0为大气压强),温度为297K,现缓慢加热汽缸内气体,直至399.3K。求:
(1)活塞刚离开B处时的温度TB;
(2)缸内气体最后的压强p;
(3)在右图中画出整个过程的p-V图线。
解析:(1)=,TB=333K,
(2)=,p=1.1p0,
(3)图略。
46.(07海南卷) ⑴有以下说法:
A.气体的温度越高,分子的平均动能越大
B.即使气体的温度很高,仍有一些分子的运动速率是非常小的
C.对物体做功不可能使物体的温度升高
D.如果气体分子间的相互作用力小到可以忽略不计,则气体的内能只与温度有关
 E.一由不导热的器壁做成的容器,被不导热的隔板分成甲、乙两室。甲室中装有一定质量的温度为T的气体,乙室为真空,如图所示。提起隔板,让甲室中的气体进入乙室。若甲室中的气体的内能只与温度有关,则提起隔板后当气体重新达到平衡时,其温度仍为T
E.一由不导热的器壁做成的容器,被不导热的隔板分成甲、乙两室。甲室中装有一定质量的温度为T的气体,乙室为真空,如图所示。提起隔板,让甲室中的气体进入乙室。若甲室中的气体的内能只与温度有关,则提起隔板后当气体重新达到平衡时,其温度仍为T
F.空调机作为制冷机使用时,将热量从温度较低的室内送到温度较高的室外,所以制冷机的工作是不遵守热力学第二定律的
G.对于一定量的气体,当其温度降低时,速率大的分子数目减少,速率小的分子数目增加
H.从单一热源吸取热量使之全部变成有用的机械功是不可能的
其中正确的是
⑵如图,在大气中有一水平放置的固定圆筒,它由a、b和c三个粗细不同的部分连接而成,各部分的横截面积分别为2S、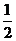 S和S。已知大气压强为p0,温度为T0.两活塞A和B用一根长为4l的不可伸长的轻线相连,把温度为T0的空气密封在两活塞之间,此时两活塞的位置如图所示。现对被密封的气体加热,使其温度缓慢上升到T。若活塞与圆筒壁之间的摩擦可忽略,此时两活塞之间气体的压强可能为多少?
S和S。已知大气压强为p0,温度为T0.两活塞A和B用一根长为4l的不可伸长的轻线相连,把温度为T0的空气密封在两活塞之间,此时两活塞的位置如图所示。现对被密封的气体加热,使其温度缓慢上升到T。若活塞与圆筒壁之间的摩擦可忽略,此时两活塞之间气体的压强可能为多少?
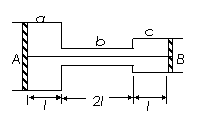
解析:⑴ABEG
⑵设加热前,被密封气体的压强为p1,轻线的张力为f,根据平衡条件有:
对活塞A: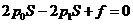
对活塞B: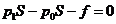
解得:p1=p0
f=0
即被密封气体的压强与大气压强相等,轻线处在拉直的松弛状态,这时气体的体积为:
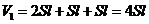
对气体加热时,被密封气体温度缓慢升高,两活塞一起向左缓慢移动,气体体积增大,压强保持p1不变,若持续加热,此过程会一直持续到活塞向左移动的距离等于l为止,这时气体的体积为:
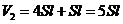
根据盖·吕萨克定律得:
解得: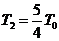
由此可知,当T≤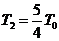 时,气体的压强为:p2=p0
时,气体的压强为:p2=p0
当T>T2时,活塞已无法移动,被密封气体的体积保持V2不变,由查理定律得:
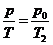
解得: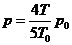
即当T>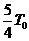 时,气体的压强为
时,气体的压强为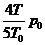
45.

 (07上海理科综合)右图a、b是某类潮汐发电示意图。涨潮时开闸,水由通道进入海湾水库蓄水,待水面升至最高点时关闭闸门(见图a)。当落潮时,开闸放水发电(见图b)。设海湾水库面积为5.0×108 m2,平均潮差为3.0 m,一天涨落潮两次,发电的平均能量转化率为10%,则一天内发电的平均功率约为 (ρ海水取1.0×103
kg/m3,g取10 m/s2)
(07上海理科综合)右图a、b是某类潮汐发电示意图。涨潮时开闸,水由通道进入海湾水库蓄水,待水面升至最高点时关闭闸门(见图a)。当落潮时,开闸放水发电(见图b)。设海湾水库面积为5.0×108 m2,平均潮差为3.0 m,一天涨落潮两次,发电的平均能量转化率为10%,则一天内发电的平均功率约为 (ρ海水取1.0×103
kg/m3,g取10 m/s2)
A.2.6×104 kW B.5.2×104 kW
 C.2.6×105
kW D.5.2×105 kW
C.2.6×105
kW D.5.2×105 kW
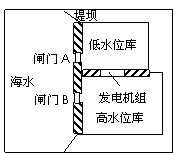
⑶右图为双水库潮汐电站原理示意图。两个水库之间始终保持着水位差,可以全天发电。涨潮时,闸门的开关情况是 ;落潮时闸门的开关情况是 。从能量的角度说,该电站是将海水的 转化为水轮机的动能,再推动发电机发电
44.(05夏季高考物理广东卷)封闭在气缸内一定质量的气体,如果保持气体体积不变,当温度升高时,以下说法正确的是 ( )
A.气体的密度增大
B.气体的压强增大
C.气体分子的平均动能减小
D.每秒撞击单位面积器壁的气体分子增多
答案:BD
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com