
常见图像变化规律:(注意平移变化能够用向量的语言解释,和按向量平移联系起来思考)
平移变换 y=f(x)→y=f(x+a),y=f(x)+b
注意:(ⅰ)有系数,要先提取系数。如:把函数y=f(2x)经过 平移得到函数y=f(2x+4)的图象。
(ⅱ)会结合向量的平移,理解按照向量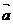 (m,n)平移的意义。
(m,n)平移的意义。
对称变换 y=f(x)→y=f(-x),关于y轴对称
y=f(x)→y=-f(x) ,关于x轴对称
y=f(x)→y=f|x|,把x轴上方的图象保留,x轴下方的图象关于x轴对称
y=f(x)→y=|f(x)|把y轴右边的图象保留,然后将y轴右边部分关于y轴对称。
(注意:它是一个偶函数)
伸缩变换:y=f(x)→y=f(ωx),
y=f(x)→y=Af(ωx+φ)具体参照三角函数的图象变换。
一个重要结论:若f(a-x)=f(a+x),则函数y=f(x)的图像关于直线x=a对称;
函数的单调性、奇偶性、周期性
单调性:定义:注意定义是相对与某个具体的区间而言。
判定方法有:定义法(作差比较和作商比较)
导数法(适用于多项式函数)
复合函数法和图像法。
应用:比较大小,证明不等式,解不等式。
奇偶性:定义:注意区间是否关于原点对称,比较f(x) 与f(-x)的关系。f(x) -f(-x)=0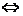 f(x) =f(-x)
f(x) =f(-x) 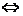 f(x)为偶函数;
f(x)为偶函数;
f(x)+f(-x)=0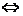 f(x) =-f(-x)
f(x) =-f(-x) 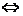 f(x)为奇函数。
f(x)为奇函数。
判别方法:定义法, 图像法 ,复合函数法
应用:把函数值进行转化求解。
周期性:定义:若函数f(x)对定义域内的任意x满足:f(x+T)=f(x),则T为函数f(x)的周期。
其他:若函数f(x)对定义域内的任意x满足:f(x+a)=f(x-a),则2a为函数f(x)的周期.
应用:求函数值和某个区间上的函数解析式。
相同函数的判断方法:① ;②
(1)函数解析式的求法:
①定义法(拼凑):②换元法:③待定系数法:④赋值法:
(2)函数定义域的求法:
①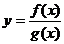 ,则g(x)
,则g(x) ; ②
; ②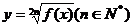 则f(x)
则f(x)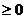 ;
;
③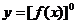 ,则f(x)
,则f(x) ; ④如:
; ④如: ,则
,则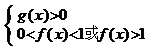 ;
;
⑤含参问题的定义域要分类讨论;
⑥对于实际问题,在求出函数解析式后;必须求出其定义域,此时的定义域要根据实际意义来确定。如:已知扇形的周长为20,半径为 ,扇形面积为
,扇形面积为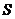 ,则
,则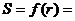 r;定义域为
。
r;定义域为
。
(3)函数值域的求法:
①配方法:转化为二次函数,利用二次函数的特征来求值;常转化为型如: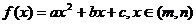 的形式;
的形式;
②逆求法(反求法):通过反解,用 来表示
来表示 ,再由
,再由 的取值范围,通过解不等式,得出
的取值范围,通过解不等式,得出 的取值范围;常用来解,型如:
的取值范围;常用来解,型如: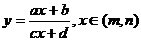 ;
;
④换元法:通过变量代换转化为能求值域的函数,化归思想;
⑤三角有界法:转化为只含正弦、余弦的函数,运用三角函数有界性来求值域;
⑥基本不等式法:转化成型如: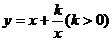 ,利用平均值不等式公式来求值域;
,利用平均值不等式公式来求值域;
⑦单调性法:函数为单调函数,可根据函数的单调性求值域。
⑧数形结合:根据函数的几何图形,利用数型结合的方法来求值域。
求下列函数的值域:①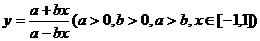 (2种方法);
(2种方法);
②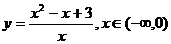 (2种方法);③
(2种方法);③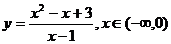 (2种方法);
(2种方法);
(1)映射的概念: (2)一一映射:(3)函数的概念:
如:若 ,
, ;问:
;问: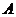 到
到 的映射有3
的映射有3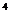 个,
个, 到
到 的映射有4
的映射有4 个;
个; 到
到 的函数有81个,若
的函数有81个,若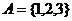 ,则
,则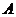 到
到 的一一映射有 个。
的一一映射有 个。
函数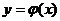 的图象与直线
的图象与直线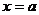 交点的个数为 个。
交点的个数为 个。
24.已知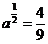 (a>0) ,则
(a>0) ,则 .
.
25已知函数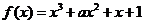 ,
,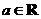 .
.
(Ⅰ)讨论函数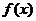 的单调区间;
的单调区间;
(Ⅱ)设函数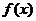 在区间
在区间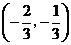 内是减函数,求
内是减函数,求 的取值范围.
的取值范围.
23.已知函数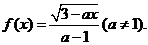
(1)若a>0,则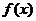 的定义域是
;
的定义域是
;
(2) 若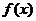 在区间
在区间 上是减函数,则实数a的取值范围是
.
上是减函数,则实数a的取值范围是
.
22. 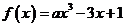 对于
对于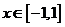 总有
总有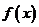 ≥0 成立,则
≥0 成立,则 = .
= .
21.直线 是曲线
是曲线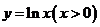 的一条切线,则实数b= ..
的一条切线,则实数b= ..
20.函数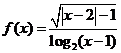 的定义域为
.
的定义域为
.
19.设函数f(x)是定义在R上的奇函数,若当x∈(0,+∞)时,f(x)=lg x,则满足f(x)>0的x的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com