
7.(2008·青岛质检)计算(log3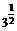 )2-
)2- +log0.25
+log0.25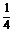 +9log5
+9log5 -log
-log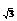 1= .
1= .
答案 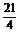
6.函数f(x)=ax+loga(x+1)在[0,1]上的最大值和最小值之和为a,则a的值为 ( )
A.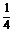 B.
B. C.2
D.4
C.2
D.4
答案?B
5.(2009·菏泽模拟)已知f(x)=ax-2,g(x)=loga|x|(a>0且a≠1),若f(4)g(-4)<0,则y=f(x),y=g(x)在同一坐标系内的图象大致是 ( )

答案?B?
4.函数y=log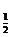 (x2-3x+2)的递增区间是
( )
(x2-3x+2)的递增区间是
( )
A.(-∞,1)
B. (2,+∞)
C. (-∞,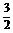 )
D.(
)
D.( 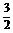 , +∞)
, +∞)
答案?A
3.已知点(m,n)在函数f(x)=ax的图象上,则下列哪个点一定在函数g(x)=-logax (a>0,a≠1)的图象上 ( )
A.(n,m) B.(n,-m) C.(m, -n) D.(-m, n)
答案 B
2.设a>1,函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为 ,则a等于
( )
,则a等于
( )
A.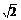 B. 2 C. 2
B. 2 C. 2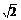 D.4
D.4
答案 D
1.若函数y=loga(x+b) (a>0,且a≠1)的图象过两点(-1,0)和(0,1),则 ( )
A.a=2,b=2?
B.a=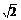 ,b=2
?C.a=2,b=1?
D.a=
,b=2
?C.a=2,b=1?
D.a=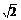 ,b=
,b=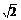
答案?A?
4.已知函数f(x)=log2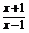 +log2(x-1)+log2(p-x).
+log2(x-1)+log2(p-x).
(1)求f(x)的定义域;
(2)求f(x)的值域.
解 (1)f(x)有意义时,有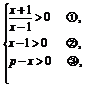
由①、②得x>1,由③得x<p,因为函数的定义域为非空数集,故p>1,f(x)的定义域是(1,p).
(2)f(x)=log2[(x+1)(p-x)]
=log2[-(x-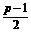 )2+
)2+ ] (1<x<p),
] (1<x<p),
①当1< <p,即p>3时,
<p,即p>3时,
0<-(x-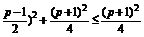 ,
,
∴log2 ≤2log2(p+1)-2.
≤2log2(p+1)-2.
②当 ≤1,即1<p≤3时,
≤1,即1<p≤3时,
∵0<-(x-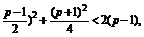
∴log2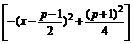 <1+log2(p-1).
<1+log2(p-1).
综合①②可知:
当p>3时,f(x)的值域是(-∞,2log2(p+1)-2];
当1<p≤3时, f(x)的值域是(-∞,1+log2(p-1)).

3.已知函数f(x)=log2(x2-ax-a)在区间(-∞,1-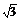 ]上是单调递减函数.求实数a的取值范围.
]上是单调递减函数.求实数a的取值范围.
解 令g(x)=x2-ax-a,
则g(x)=(x-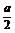 )2-a-
)2-a- ,
,
由以上知g(x)的图象关于直线x=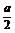 对称且此抛物线开口向上.
对称且此抛物线开口向上.
因为函数f(x)=log2g(x)的底数2>1,
在区间(-∞,1-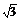 ]上是减函数,
]上是减函数,
所以g(x)=x2-ax-a在区间(-∞,1-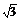 ]上也是单调减函数,且g(x)>0.
]上也是单调减函数,且g(x)>0.
∴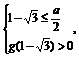 即
即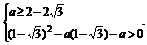
解得2-2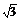 ≤a<2.
≤a<2.
故a的取值范围是{a|2-2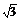 ≤a<2}.
≤a<2}.
2.已知0<a<1,b>1,ab>1,则loga ,logab,logb
,logab,logb 的大小关系是
( ) A.loga
的大小关系是
( ) A.loga <logab<logb
<logab<logb
?B.logab<loga <logb
<logb
?C.logab<logb <loga
<loga
?D.logb <loga
<loga <logab
<logab
答案?C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com