
6.已知f(x)=1-(x-a)(x-b) (a<b),m,n是f(x)的零点,且m<n,则实数a,b,m,n的大小关系是 ( )
A. m<a<b<n B. a<m<n<b C.a<m<b<n D.m<a<n<b
答案?A
5.若函数f(x)=x3-3x+a有3个不同的零点,则实数a的取值范围是 ( )
A. (-2,2)?
B.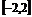 C.(-∞,-1)
D.(1,+ ∞)
C.(-∞,-1)
D.(1,+ ∞)
答案?A
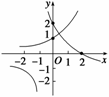
4.f(x)=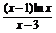 的零点个数为
( )
的零点个数为
( )
A.1 B.2 C.3 D.0
答案?A
3.设函数y=x3与y=(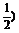 x-2的图象交点为(x0,y0),则x0所在的区间是 ( )
x-2的图象交点为(x0,y0),则x0所在的区间是 ( )
A.(0,1) B. (1,2) C.(2,3) D.(3,4)
答案?B
2.如图所示的函数图象与x轴均有交点,其中不能用二分法求图中交点横坐标的是 ( )
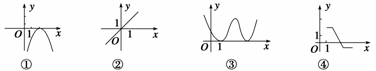
A.①② B.①③ C.①④ D.③④
答案?B?
1.下列函数中在区间[1,2]上有零点的是 ( )
A.f(x)=3x2-4x+5 B.f(x)=x3-5x-5
C.f(x)=mx-3x+6? D.f(x)=ex+3x-6
答案?D
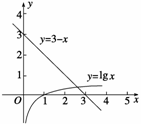
4.利用计算器,求方程lgx=3-x的近似解.(精确到0.1)
解 如图,由函数y=lgx与y=3-x的图象可以发现,方程lgx=3-x有唯一解,记为x1,
并且这个解在区间(2,3)内.
 设f(x)=lgx+x-3,用计算器计算,得:
设f(x)=lgx+x-3,用计算器计算,得:
f(2)<0,f(3)>0 x1∈(2,3)
x1∈(2,3)
f(2.5)<0,f(3)>0 x1∈(2.5,3)
x1∈(2.5,3)
f(2.5)<0,f(2.75)>0 x1∈(2.5,2.75),
x1∈(2.5,2.75),
f(2.5)<0,f(2.625)>0 x1∈(2.5,2.625),
x1∈(2.5,2.625),
f(2.562 5)<0,f(2.625)>0 x1∈(2.562 5,2.625).
x1∈(2.562 5,2.625).
因为2.625与2.562 5精确到0.1的近似值都为2.6,所以原方程的近似解为:x1≈2.6.

3.已知函数f(x)=x2+(a2-1)x+(a-2)的一个零点比1大,一个零点比1小,求实数a的取值范围.
解 方法一 设方程x2+(a2-1)x+(a-2)=0的两根分别为x1,x2 (x1<x2),
则(x1-1)(x2-1)<0,∴x1·x2-(x1+x2)+1<0,
由韦达定理得(a-2)+(a2-1)+1<0,
即a2+a-2<0,∴-2<a<1.
方法二 函数的大致图象如图所示,
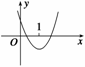 则有f(1)<0,即1+(a2-1)+a-2<0,
则有f(1)<0,即1+(a2-1)+a-2<0,
a2+a-2<0,∴-2<a<1.
2.已知函数f(x)=ax+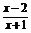 (a>1),判断f(x)=0的根的个数.
(a>1),判断f(x)=0的根的个数.
 解 设f1(x)=ax (a>1),f2(x)=-
解 设f1(x)=ax (a>1),f2(x)=-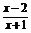 ,则f(x)=0的解即为f1(x)=f2(x)的解,即为函数f1(x)与f2(x)
,则f(x)=0的解即为f1(x)=f2(x)的解,即为函数f1(x)与f2(x)
图象交点的横坐标.在同一坐标系中,作出函数f1(x)=ax(a>1)与f2(x)=-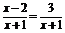 -1的图象
-1的图象
(如图所示).
两函数图象有且只有一个交点,即方程f(x)=0有且只有一个根.
1.求下列函数的零点:
(1)y=x3-7x+6;(2)y=x+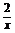 -3.
-3.
解(1)∵x3-7x+6=(x3-x)-(6x-6)
=x(x2-1)-6(x-1)=x(x+1)(x-1)-6(x-1)
=(x-1)(x2+x-6)=(x-1)(x-2)(x+3)
解x3-7x+6=0,即(x-1)(x-2)(x+3)=0
可得x1=-3,x2=1,x3=2.
∴函数y=x3-7x+6的零点为-3,1,2.
(2)∵x+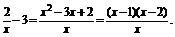
解x+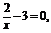 即
即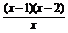 =0,可得x=1或x=2.
=0,可得x=1或x=2.
∴函数y=x+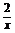 -3的零点为1,2.
-3的零点为1,2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com