
4.某工厂生产某种产品固定成本为2 000万元,并且每生产一单位产品,成本增加10万元.又知总收入K是单位产品数Q的函数,K(Q)=40Q-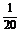 Q2,则总利润L(Q)的最大值是 万元.
Q2,则总利润L(Q)的最大值是 万元.
答案 2 500

例1如图所示,在矩形ABCD中,已知AB=a,BC=b(b<a),在AB,AD,CD,CB上分别截取AE,AH,CG,CF都等于x,当x为何值时,四边形EFGH的面积最大?并求出最大面积.
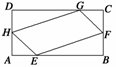 解 设四边形EFGH的面积为S,
解 设四边形EFGH的面积为S,
则S△AEH=S△CFG= x2,
x2,
S△BEF=S△DGH= (a-x)(b-x),
(a-x)(b-x),
∴S=ab-2[ 2+
2+ (a-x)(b-x)]
(a-x)(b-x)]
=-2x2+(a+b)x=-2(x-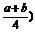 2+
2+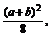
由图形知函数的定义域为{x|0<x≤b}.
又0<b<a,∴0<b<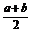 ,若
,若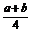 ≤b,即a≤3b时,
≤b,即a≤3b时,
则当x=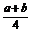 时,S有最大值
时,S有最大值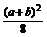 ;
;
若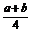 >b,即a>3b时,
>b,即a>3b时,
S(x)在(0,b]上是增函数,
此时当x=b时,S有最大值为
-2(b-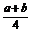 )2+
)2+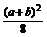 =ab-b2,
=ab-b2,
综上可知,当a≤3b,x=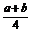 时,
时,
四边形面积Smax=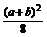 ,
,
当a>3b,x=b时,四边形面积Smax=ab-b2.
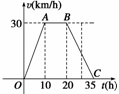 例2据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度
例2据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度
v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴
的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过
的路程s(km).
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
解 (1)由图象可知:
当t=4时,v=3×4=12,
∴s= ×4×12=24.
×4×12=24.
(2)当0≤t≤10时,s= ·t·3t=
·t·3t=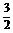 t2,
t2,
当10<t≤20时,s= ×10×30+30(t-10)=30t-150;
×10×30+30(t-10)=30t-150;
当20<t≤35时,s= ×10×30+10×30+(t-20)×30-
×10×30+10×30+(t-20)×30- ×(t-20)×2(t-20)=-t2+70t-550.
×(t-20)×2(t-20)=-t2+70t-550.
综上可知s=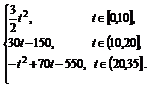
(3)∵t∈[0,10]时,smax=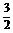 ×102=150<650.
×102=150<650.
t∈(10,20]时,smax=30×20-150=450<650.
∴当t∈(20,35]时,令-t2+70t-550=650.
解得t1=30,t2=40,∵20<t≤35,
∴t=30,所以沙尘暴发生30 h后将侵袭到N城.
例3(12分)1999年10月12日“世界60亿人口日”,提出了“人类对生育的选择将决定世界未来”的主题,控制人口急剧增长的紧迫任务摆在我们的面前.
(1)世界人口在过去40年内翻了一番,问每年人口平均增长率是多少?
(2)我国人口在1998年底达到12.48亿,若将人口平均增长率控制在1%以内,我国人口在2008年底至多有多少亿?
以下数据供计算时使用:
|
l
数N |
l
1.010 |
l
1.015 |
l
1.017 |
l
1.310 |
l
2.000 |
|
l
对数lgN |
l
0.004 3 |
l
0.006 5 |
l
0.007 3 |
l
0.117 3 |
l
0.301 0 |
|
l
数N |
l
3.000 |
l
5.000 |
l
12.48 |
l
13.11 |
l
13.78 |
|
l
对数lgN |
l
0.477 1 |
l
0.699 0 |
l
1.096 2 |
l
1.117 6 |
l
1.139 2 |
解 (1)设每年人口平均增长率为x,n年前的人口数为y,
则y·(1+x)n=60,则当n=40时,y=30,
即30(1+x)40=60,∴(1+x)40=2, 4分
两边取对数,则40lg(1+x)=lg2,
则lg(1+x)=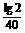 =0.007 525,
=0.007 525,
∴1+x≈1.017,得x=1.7%. 8分
(2)依题意,y≤12.48(1+1%)10?,
得lgy≤lg12.48+10×lg1.01=1.139 2,
∴y≤13.78,故人口至多有13.78亿. 11分
答 每年人口平均增长率为1.7%,2008年底人口至多有13.78亿. 12分

3.已知光线每通过一块玻璃板,光线的强度要损失10%,要使通过玻璃板的光线的强度减弱到原来强度的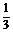 以下,则至少需要重叠玻璃板数为 (
)
以下,则至少需要重叠玻璃板数为 (
)
A.8块 B.9块 C.10块 D.11块
答案 D
2.我国为了加强对烟酒生产的宏观调控,除了应征税外还要征收附加税,已知某种酒每瓶售价为70元,不收附加税时,每年大约销售100万瓶,若每销售100元国家要征附加税为x元(税率x%),则每年销售量减少10x万瓶,为了要使每年在此项经营中收取的附加税额不少于112万元,则x的最小值为 ( )
A.2 B.6 C.8 D.10
答案?A?
1.一等腰三角形的周长是20,底边y是关于腰长x的函数,它的解析式为 ( )
A.y=20-2x(x≤10) B.y=20-2x(x<10)
C.y=20-2x(5≤x≤10) D.y=20-2x(5<x<10)
答案?D
12.已知a、b是不全为0的实数,求证:方程3ax2+2bx-(a+b)=0在(0,1)内一定有实根.
证明 若a=0时,则b≠0,
此时方程的根为x= ,满足题意.
,满足题意.
当a≠0时,令f(x)=3ax2+2bx-(a+b).
(1)若a(a+b)<0,
则f(0)·f( )=-(a+b)·(-
)=-(a+b)·(-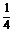 a)=
a)=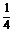 a(a+b)<0,
a(a+b)<0,
所以f(x)在区间(0,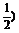 内有一实根.
内有一实根.
(2)若a(a+b)≥0,
则f(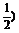 f(1)=(-
f(1)=(-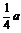 )(2a+b)
)(2a+b)
=-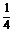 a2-
a2-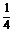 a(a+b)<0,
a(a+b)<0,
所以f(x)在区间( ,1)内有一实根.
,1)内有一实根.
综上所述,方程3ax2+2bx-(a+b)=0在(0,1)内一定有实根.
§2.8 函数模型及其应用
 基础自测
基础自测
11.关于x的二次方程x2+(m-1)x+1=0在区间[0,2]上有解,求实数m的取值范围.
解 设f(x)=x2+(m-1)x+1,x∈[0,2],
①若f(x)=0在区间[0,2]上有一解,
∵f(0)=1>0,则应有f(2)≤0,
又∵f(2)=22+(m-1)×2+1,∴m≤-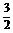 .
.
②若f(x)=0在区间[0,2]上有两解,则
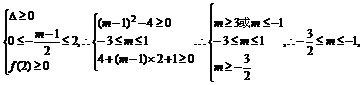
由①②可知m≤-1.
10.若关于x的方程3x2-5x+a=0的一个根在(-2,0)内,另一个根在(1,3)内,求a的取值范围.
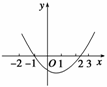 解 设f(x)=3x2-5x+a,则f(x)为开口向上的抛物线(如图所示).
解 设f(x)=3x2-5x+a,则f(x)为开口向上的抛物线(如图所示).
∵f(x)=0的两根分别在区间(-2,0),(1,3)内,
∴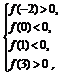 即
即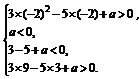
解得-12<a<0.所求a的取值范围是(-12,0).
9.已知二次函数f(x)=4x2-2(p-2)x-2p2-p+1在区间[-1,1]内至少存在一个实数c,使f(c)>0,求实数p的取值范围.
解 二次函数f(x)在区间[-1,1]内至少存在一个实数c,使f(c)>0的否定是对于区间[-1,1]内的任意一个x都有f(x)≤0,
∴ 即
即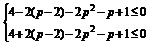
整理得: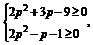 解得:p
解得:p 或p
或p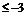 .
.
∴二次函数在区间[-1,1]内至少存在一个实数c,使f(c)>0的实数p的取值范围是(-3,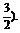
8.关于x的实系数方程x2-ax+2b=0的一根在区间[0,1]上,另一根在区间[1,2]上,则2a+3b的最大
值为 .
答案 9
7.若函数f(x)=x2-ax-b的两个零点是2和3,则函数g(x)=bx2-ax-1的零点是 .
答案 - ,-
,-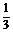
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com