
7.某种商品进货单价为40元,若按每个50元的价格出售,能卖出50个,若销售单价每上涨1元,则销售
量就减少1个,为了获得最大利润,此商品的最佳售价应定为 元.
答案 70
6.某商店计划投入资金20万元经销甲、乙两种商品,已知经销甲商品与乙商品所获得的利润分别为P(万元)和Q(万元),且它们与投入资金x(万元)的关系是:P= ,Q=
,Q= (a>0).若不管资金如何投放,经销这两种商品或其中一种商品所获得的纯利润总和不少于5万元,则a的最小值应为
( )
(a>0).若不管资金如何投放,经销这两种商品或其中一种商品所获得的纯利润总和不少于5万元,则a的最小值应为
( )
A. B.5
C.
B.5
C. D.-
D.-
答案 A
5.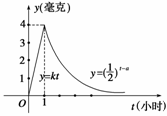 某医药研究所开发一种新药,如果成年人按规定的剂量服用,据检测,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的关系用如图所示曲线表示.据进一步测定,每毫升血液中含药量不少于0.25毫克时,治疗疾病有效,则服药一次治疗该疾病有效的时间为(小时)为
( )
某医药研究所开发一种新药,如果成年人按规定的剂量服用,据检测,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的关系用如图所示曲线表示.据进一步测定,每毫升血液中含药量不少于0.25毫克时,治疗疾病有效,则服药一次治疗该疾病有效的时间为(小时)为
( )
A.4
B. 4
C. 4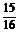 D.5
D.5
答案?C
4.某产品的总成本y(万元)与产量x(台)之间的函数关系式是y=3 000+20x-0.1x2,x∈(0,240),若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总成本)的最低产量为 ( ).
A. 100台 B.120台 C.150台 D.180台
答案 C
3.某工厂8年来某种产品的总产量C与时间t(年)的函数关系如图所示,下列四种说法:
 ①前三年中,产量增长的速度越来越快;
①前三年中,产量增长的速度越来越快;
②前三年中,产量增长的速度越来越慢;
③第三年中,产品停止生产;
④第三年中,这种产品产量保持不变.
其中说法正确的是 ( )
A.②与③ B.②与④ C.①与③ D.①与④
答案?A
2.某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,
现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,
当截取的矩形面积最大时,矩形两边长x,y应为 ( )
A. x=15,y=12 B.x=12,y=15 C. x=14,y=10 D. x=10,y=14
答案 A
1.某机床在生产中所需垫片可以外购,也可自己生产,其中外购的单价是每个1.10元,若自己生产,则每月需投资固定成本800元,并且每生产一个垫片还需材料费和劳务费共0.60元.设该厂每月所需垫片x个,则自己生产垫片比外购垫片较合算的条件是 ( )
A.x>1 800 B.x>1 600 C.x>500 D.x>1 400
 答案 B
答案 B
3.某工厂今年1月、2月、3月生产某产品分别为1万件、1.2万件、1.3万件.为了估测以后每个月的产量,以这三个月的产品数量为依据,用一个函数模型来模拟该产品的月产量y与月份数x的关系.模拟函数可以选用二次函数f(x)或函数g(x)=abx+c(其中a、b、c为常数).已知4月份该产品的产量为1.37万件.请问用以上哪个函数作为函数模型较好?并说明理由.
解 设f(x)=px2+qx+r(p≠0),则有
 解得p=-0.05,q=0.35,r=0.7.
解得p=-0.05,q=0.35,r=0.7.
∴f(4)=-0.05×42+0.35×4+0.7=1.3.
又
解得a=-0.8,b=0.5,c=1.4.
∴g(4)=-0.8×0.54+1.4=1.35.
经比较可知,用g(x)=-0.8×(0.5)x+1.4作为模拟函数较好.

2.某工厂生产一种机器的固定成本(即固定投入)为0.5万元,但每生产100台,需要加可变成本(即另增加投入)0.25万元.市场对此产品的年需求量为500台,销售的收入函数为R(x)=5x- (万元)(0≤x≤5),其中x是产品售出的数量(单位:百台).
(万元)(0≤x≤5),其中x是产品售出的数量(单位:百台).
(1)把利润表示为年产量的函数;
(2)年产量是多少时,工厂所得利润最大?
(3)年产量是多少时,工厂才不亏本?
解 (1)当x≤5时,产品能售出x百台;
当x>5时,只能售出5百台,
故利润函数为L(x)=R(x)-C(x)
=
(2)当0≤x≤5时,L(x)=4.75x- -0.5,
-0.5,
当x=4.75时,L(x)max=10.781 25万元.
当x>5时,L(x)=12-0.25x为减函数,
此时L(x)<10.75(万元).∴生产475台时利润最大.
(3)由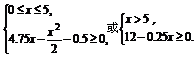
得x≥4.75- =0.1(百台)或x<48(百台).
=0.1(百台)或x<48(百台).
∴产品年产量在10台至4 800台时,工厂不亏本.
1.某商人将进货单价为8元的某种商品按10元一个销售时,每天可卖出100个,现在他采用提高售价,减少进货量的办法增加利润,已知这种商品销售单价每涨1元,销售量就减少10个,问他将售价每个定为多少元时,才能使每天所赚的利润最大?并求出最大值.
解 设每个提价为x元(x≥0),利润为y元,每天销售总额为(10+x)(100-10x)元,
进货总额为8(100-10x)元,
显然100-10x>0,即x<10,
则y=(10+x)(100-10x)-8(100-10x)=(2+x)(100-10x)=-10(x-4)2+360 (0≤x<10).
当x=4时,y取得最大值,此时销售单价应为14元,最大利润为360元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com