
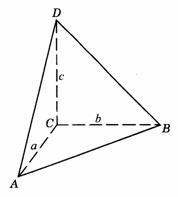
472. 已知D为平面ABC外一点,且DA、DB、DC两两垂直.求证:顶点D所对的三角形面积的平方等于其余三个三角形面积的平方和,即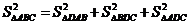 .
.
解析:如图答9-25,设DA=a,DB=b,DC=c,则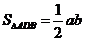 ,
,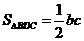 ,
,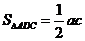 .在△ABD中,作DM⊥AB于M,则
.在△ABD中,作DM⊥AB于M,则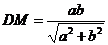 . ∵ CD⊥AD,CD⊥DB,∴
CD⊥平面ADB,∴
CD⊥DM.在Rt△CDM中,
. ∵ CD⊥AD,CD⊥DB,∴
CD⊥平面ADB,∴
CD⊥DM.在Rt△CDM中,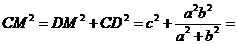
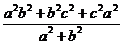 , ∴
, ∴ 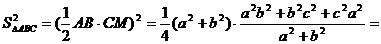
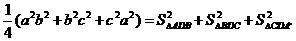
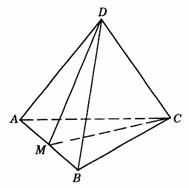
图答9-25
471. 在△ABC中,∠ACB=90°,CD⊥平面ABC.求证:△ABD是锐角三角形.
解析:如图答9-24,设AC=a,BC=b,CD=c,∵ △ACD是Rt△,∴ 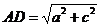 . ∵ △ABC是Rt△,∴
. ∵ △ABC是Rt△,∴ 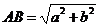 .∵ △BCD是Rt△,∴
.∵ △BCD是Rt△,∴ 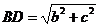 .而在
.而在
△ABD中,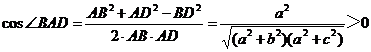 ,又∵ ∠BAD是三角形内角,∴
0°<∠BAD<180°,∴ ∠BAD是锐角,同理∠ABD、∠ADB是锐角,∴
△ABD是锐角三角形.
,又∵ ∠BAD是三角形内角,∴
0°<∠BAD<180°,∴ ∠BAD是锐角,同理∠ABD、∠ADB是锐角,∴
△ABD是锐角三角形.
470. 如图9-55,将边长为a的正三角形ABC按它的高AD为折痕折成一个二面角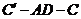 .
.
(1)指出这个二面角的面、棱、平面角;
(2)若二面角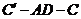 是直二面角,求
是直二面角,求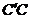 的长;
的长;
(3)求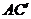 与平面
与平面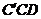 所成的角;
所成的角;
(4)若二面角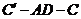 的平面角为120°,求二面角
的平面角为120°,求二面角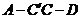 的平面角的正切值.
的平面角的正切值.
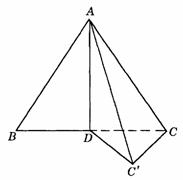
解析:(1)∵ AD⊥BC,∴ AD⊥DC,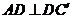 ,∴ 二面角
,∴ 二面角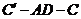 的面为ADC和面
的面为ADC和面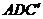 ,棱为AD,二面角的平面角为
,棱为AD,二面角的平面角为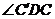 .
.
(2)若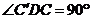 ,∵ AC=a,∴
,∵ AC=a,∴ 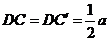 ,∴
,∴ 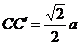 .
.
(3)∵ 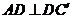 ,AD⊥DC,∴ AD⊥平面
,AD⊥DC,∴ AD⊥平面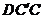 .∴
.∴  为
为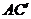 与平面
与平面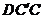 所成的角,在Rt△
所成的角,在Rt△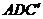 中,
中,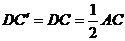 ,∴
,∴ 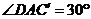 ,于是
,于是
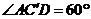 .
.
(4)取 的中点E,连结AE、DE,∵
的中点E,连结AE、DE,∵ 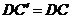 ,
,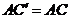 ,∴
,∴ 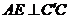 ,
,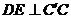 ,∴ ∠AED为二面角
,∴ ∠AED为二面角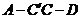 的平面角,∵
的平面角,∵ 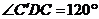 ,
,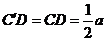 ,∴
,∴ 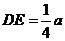 ,在Rt△AED中,
,在Rt△AED中,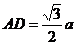 ,∴
,∴ 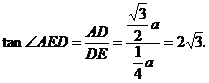
469. 在正方体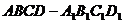 中,
中,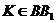 ,
,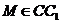 ,且
,且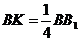 ,
,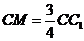 (如图9-54).求:平面AKM与ABCD所成角的大小.
(如图9-54).求:平面AKM与ABCD所成角的大小.
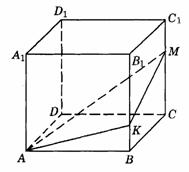
解析:由于BCMK是梯形,则MK与CB相交于E.A、E确定的直线为l,过C作CF⊥l于F,连结MF,因为MC⊥平面ABCD,CF⊥l,故MF⊥l.∠MFC是二面角M-l-C的平面角.设正方体棱长为a,则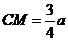 ,
,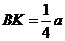 .在△ECM中,由BK∥CM可得
.在△ECM中,由BK∥CM可得 ,
,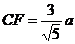 ,故
,故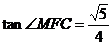 .因此所求角的大小为
.因此所求角的大小为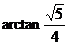 或
或 .
.
468. .如图9-53, 是长方体,AB=2,
是长方体,AB=2,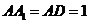 ,求二平面
,求二平面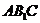 与
与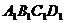 所成二面角的大小.
所成二面角的大小.

解析:∵ 平面ABCD∥平面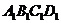 ,∴ 平面
,∴ 平面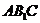 与平面
与平面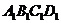 的交线l为过点
的交线l为过点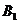 且平行于AC的直线.直线l就是二平面
且平行于AC的直线.直线l就是二平面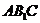 与
与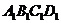 所成二面角的棱.又
所成二面角的棱.又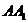 ⊥平面
⊥平面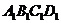 ,过
,过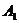 作AH⊥l于H,连结AH.则
作AH⊥l于H,连结AH.则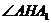 为二面角
为二面角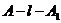 的平面角.可求得
的平面角.可求得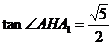 .因此所求角的大小为
.因此所求角的大小为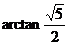 或
或
467. 平面a ⊥平面g ,平面b ⊥平面g ,且a ∩g =a,b ∩g =b,a∥b,平面a 与b 的位置关系是________.
解析:平行.在g 上作l⊥a,∵ a∥b,∴ l⊥b.∵ a ⊥g 于a,∴ l⊥a ,同理l⊥b .∴ a ∥b .
466. 已知二面角a
-l-b 的大小为q (q
是锐角),A∈l,B∈l,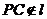 ,且P∈a
,P在b
内的射影为P′.记△ABP的面积为S,则△ABP′的面积S′等于________.
,且P∈a
,P在b
内的射影为P′.记△ABP的面积为S,则△ABP′的面积S′等于________.
解析:Scosq
.作PH⊥l于H,连结 .∵
.∵ 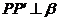 ,∴
,∴ 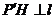 (三垂线定理的逆定理).∴
(三垂线定理的逆定理).∴ 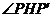 为二面角a -l-b
的平面角,即
为二面角a -l-b
的平面角,即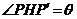 .
.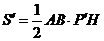 ,
,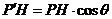 ,∴
,∴ 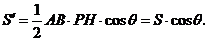
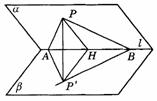
图答9-46
465. 如图9-52,A是△BCD所在平面外一点,AB=AD,∠ABC=∠ADC=90°,则二面角A-BD-C的平面角是( ).
A.钝角 B.直角
C.锐角 D.大小不确定的
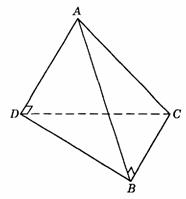
解析:A.取BD中点E,连结AE、CE,由AB=AD,∠ABC=∠ADC,AC=AC得△ABC≌△ADC,∴ DC=BC,∴ AE⊥BD,CE ⊥
BD,∴ ∠AEC为二面角A-BD-C的平面角.∵ 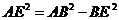 ,
,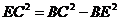 ,
,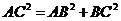 ,∴
,∴ 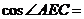
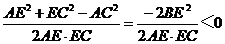 ,∵ ∠AEC为钝角
,∵ ∠AEC为钝角
464. 一条线段的两个端点分别在一个直二面角的两个面内(都不在棱上),则这条线段与这两个平面所成的角的和( ).
A.等于90° B.大于90°
C.不大于90° D.不小于90°
解析:C.如图答9-45,设直二面角a -l-b ,作AC⊥l于C,BD⊥l于D.∵ a ⊥b ,则AC⊥b ,BD⊥a ,连结BC、AD,则∠ABC为AB与平面b 所成的角,∠BAD为AB与平面a 所成的角.
当AB⊥l时,易得AB与a 、b
所成角之和等于90°,当AB与l不垂直时,设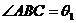 ,
,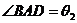 ,
,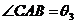 ,
,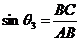 ,
,  ,∵ BC>BD,∴
,∵ BC>BD,∴ 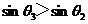 ,∵ 函数y=sinx在
,∵ 函数y=sinx在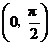 上是增函数,∴
上是增函数,∴ 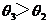 ,∵
,∵ 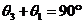 ,∴
,∴ 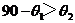 ,∴
,∴ 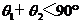 .故AB与a
、b 所成角之和≤90°.
.故AB与a
、b 所成角之和≤90°.
463. 设直线l、m,平面a
、b 、g 满足b
∩g =l,l∥a
,m a ,且m⊥g
,则必有( ).
a ,且m⊥g
,则必有( ).
A.a ⊥g ,且l⊥m B.a ⊥g ,且m∥b
C.m∥b ,且l⊥m D.a ∥b ,且a ⊥g
解析:A.
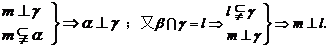
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com