
13.(城西中学)已知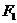 、
、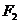 是双曲线
是双曲线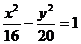 的焦点,点P是双曲线上一点,若P到焦点
的焦点,点P是双曲线上一点,若P到焦点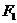 的距离为9,则P到焦点
的距离为9,则P到焦点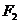 的距离为___________.
的距离为___________.
正确答案:17
错因:不注意取舍。
12.(城西中学)已知一条曲线上面的每一点到点A(0,2)的距离减去它到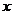 轴的距离的差都是2,则这曲线的方程是_____________
轴的距离的差都是2,则这曲线的方程是_____________
正确答案: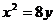 或
或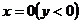
错因:数形结合时考虑不全面。
11.(城西中学)已知F1、F2是椭圆 的焦点,P是椭圆上一点,
且∠F1PF2=90°,
则椭圆的离心率e的取值范围是 。
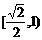
答案:
错因:范围问题主要是找不等关系式,如何寻求本题中的不等关系,忽视椭圆的范围。
10.(磨中)过点M(-1,0)的直线l1与抛物线y2=4x交于P1,P2两点,记线段P1P2的中点为P,过P和这个抛物线的焦点F的直线为l2,l1的斜率为K,试把直线l2的斜率与直线l1的斜率之比表示为k的函数,其解析式为________,此函数定义域为________。
正确答案:f(k)=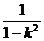 (-1,0)∪(0,1)
(-1,0)∪(0,1)
错误原因:忽视了直线l1与抛物线相交于两点的条件,得出错误的定义域。
9.(磨中)已知P是以F1、F2为焦点的双曲线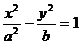 上一点,PF1⊥PF2且tan∠PF1F2=
上一点,PF1⊥PF2且tan∠PF1F2=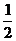 ,则此双曲线的离心率为_______________。
,则此双曲线的离心率为_______________。
正确答案: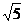
错误原因:忽视双曲线定义的应用。
8.(磨中)双曲线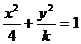 的离心率为e,且e∈(1,2)则k的范围是________。
的离心率为e,且e∈(1,2)则k的范围是________。
正确答案:k∈(-12,0)
错误原因:混淆了双曲线和椭圆的标准方程。
7.(磨中)过点(0,2)与抛物线y2=8x只有一个共点的直线有______条。
正确答案:3
错误原因:认为与抛物线只有一个共点的直线只能与抛物线相切而出错。
6.(磨中)已知双曲线的右准线为x=4,右焦点F(10,0)离心率e=2,则双曲线方程为______。
正确答案: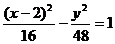
错误原因:误认为双曲线中心在原点,因此求出双曲线的标准方程而出现错误。
5.(磨中)过点(3,-3)且与圆(x-1)2+y2=4相切的直线方程是:___________。
正确答案:5x+12y+21=0或x=3
错误原因:遗漏了斜率不存在的情形造成漏解。
4.(磨中)已知直线l1:x+y-2=0 l2:7x-y+4=0 则l1与l2夹角的平分线方程为______。
正确答案:6x+2y-3=0
错语原因:忽视两直线夹角的概念多求了夹角的邻补角的平分线方程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com