
3、匀变速直线运动的速度--时间图象(υ-t图)
匀变速直线运动的速度是时间的一次函数,即
υt=υ0+at
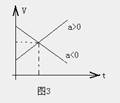 所对应的是一条直线,如图3所示。由图可求出任意时刻的速度,或根据速度求出时间,还可以求出任意时间所通过的位移,还可以求出匀变速直线运动的加速度a=△υ/△t=直线的斜率K,直线的斜率越大,
所对应的是一条直线,如图3所示。由图可求出任意时刻的速度,或根据速度求出时间,还可以求出任意时间所通过的位移,还可以求出匀变速直线运动的加速度a=△υ/△t=直线的斜率K,直线的斜率越大,
即直线越陡,则对就的加速度越大。
2、匀速直线运动的速度--时间图象(υ-t图)
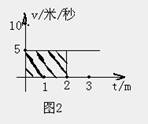
匀速运动的速度不随时间而变化,因此其图象是一条与时间轴平行的直线,如图2所示,利用υ-t图象可求出任意时刻对应的位移,也就是等于这个矩形的面积。
目的要求:
明确s-t,v-t图象的物理意义
知识要点:
1、匀速直线运动的位移--时间图象(S-t图)
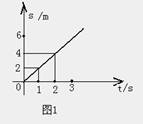
匀速直线运动的位移S与时间t成正比,即S=υt,因此其图象是过原点的直线。由图象可求出任意时间内的位移,如图1可知,1秒末图象对应的位移为2米,应用图也可以求出通过任一位移所需的时间。由图象还可以求物体匀速运动的速度。υ=△s/△t=2m/s,图中直线的斜率表示物体匀速运动的速度,K=υ=△s/△t。
2、竖直上抛运动:物体上获得竖直向上的初速度υ0后仅在重力作用下的运动。
特点:只受重力作用且与初速度方向反向,以初速方向为正方向则a=-g
 υt=υ0-gt
υt=υ0-gt
运动规律: h=υ0t-gt2/2
υt2=υt2-2gh
对于竖直上抛运动,有分段分析法和整体法两种处理方法。分段法以物体上升到最高点为运动的分界点,根据可逆性可得t上=t下=υ0/g,上升最大高度H=υ02/2g,同一高度速度大小相等,方向相反。整体法是以抛出点为计时起点,速度、位移用下列公式求解:
 υt=υ0-gt
υt=υ0-gt
h=υ0t-gt2/2
注意:若物体在上升或下落中还受有恒空气阻力,则物体的运动不再是自由落体和竖直上抛运动,分别计算上升a上与下降a下的加速度,利用匀变速运动公式问题同样可以得到解决。
例题分析:
例1、从距地面125米的高处,每隔相同的时间由静止释放一个小球队,不计空气阻力,g=10米/秒2,当第11个小球刚刚释放时,第1个小球恰好落地,试求:
(1)相邻的两个小球开始下落的时间间隔为多大?
(2)当第1个小球恰好落地时,第3个小球与第5个小球相距多远?
(拓展)将小球改为长为5米的棒的自由落体,棒在下落过程中不能当质点来处理,但可选棒上某点来研究。
例2、在距地面25米处竖直上抛一球,第1秒末及第3秒末先后经过抛出点上方15米处,试求:
(1)上抛的初速度,距地面的最大高度和第3秒末的速度;
(2)从抛出到落地所需的时间(g=10m/s2)
例3、一竖直发射的火箭在火药燃烧的2S内具有3g的竖直向上加速度,当它从地面点燃发射后,它具有的最大速度为多少?它能上升的最大高度为多少?从发射开始到上升的最大高度所用的时间为多少?(不计空气阻力。G=10m/s2)
目的要求
复习自由落体运动的规律。
知识要点:
1、自由落体运动:物体仅在重力作用下由静止开始下落的运动
特点:只受重力作用,即a=g。从静止开始,即υ0=0
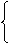 υt=gt
υt=gt
运动规律: S=gt2/2
υt2=2gh
对于自由落体运动,物体下落的时间仅与高度有关,与物体受的重力无关。
3、对于匀减速直线运动,必须特别注意其特性:
(1)匀减速直线运动总有一个速度为零的时刻,此后,有的便停下来,有些会反向匀加速
(2)匀减速运动的反向运动既可以按运动的先后顺序进行运算,也可将返回的运动按初速为零的匀加速运动计算。
例题分析:
例1、关于加速度与速度、位移的关系,以下说法正确的是:(D)
A、υ0为正,a为负,则速度一定在减小,位移也一定在减小;
B、υ0为正,a为正,则速度一定在增加,位移不一定在增加;
C、υ0与a同向,但a逐渐减小,速度可能也在减小;
D、υ0与a反向,但a逐渐增大,则速度减小得越来越快(在停止运动前)
例2、水平导轨AB的两端各有一竖直的挡板A和B,AB=4米,物体自A开始以4m/s的速度沿导轨向B运动,已知物体在碰到A或B以后,均以与挡板碰前大小相等的速度反弹回来,并且物体在导轨上作匀减速运动的加速度大小相同,为了使物体最终能停在AB的中点,则这个加速度的大小应为多少?
例3、一列车共20节车箱,它从车站匀加速开出时,前5节车厢经过站在车头旁边的人的时间为t秒,那么:
(1)第三个5节车厢经过人的时间为多少?
(2)若每节车厢长为L,则车尾经过人时的速度多大?
(3)车正中点经过人时速度为多大?
(4)车经过人身旁总时间为多少?
答案:例2:-4/(2n+1)例3:略
2、匀变速直线运动特点
(1)、做匀变速直线运动的物体,在某段时间内的平均速度等于这段时间内的中间时刻的即时速度。
(2)、匀变速直线运动某段位移中点的即时速度,等于这段位移两端的即时速度的几何平均值。
(3)、做匀变速直线运动的物体,如果在各个连续相等的时间T内的位移分别为
sⅠ,sⅡ,sⅢ,……sn 则:
△s=sⅡ-sⅠ=sⅢ-sⅡ=……=aT2
(4)、初速为零的匀变速直线运动的特征:(设t为单位时间)
①1t末,2t末,3t末……即时速度的比为:
υ1:υ2:υ3:……υn=1:2:3:……n
②1t内,2t内,3t内……位移之比为:
S1:S2:S3:……:Sn=12:22:32:……:n2
③第1t内,第2t内,第3t内……位移之比为:
SⅠ:SⅡ:SⅢ:...Sn=1:3:5:...(2n-1)

目的要求:
熟练掌握匀变速运动的规律,并能灵活运用其规律解决实际问题。

知识要点:
1、匀变速直线运动是在相等的时间里速度的变化量相等的直线运动。基本规律有:
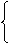 υt=υ0+at
υt=υ0+at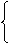
|

 s=υ0t+ at2/2
s=υ0t+ at2/2
s=υ平t

利用上面式子时要注意:
(1)、υt,υ0,υ平,a视为矢量,并习惯选υ0的方向为正方向:
(2)、其余矢量的方向与υ0相同取正值,反向取负值,若a与υ同向,物体作匀加速运动,若a与υ反向,物体作匀减速运动。
7、运动的相对性:只有在选定参照物之后才能确定物体是否在运动或作怎样的运动。一般以地面上不动的物体为参照物。

例题分析:
例1、物体M从A运动到B,前半程平均速度为υ1,后半程平均速度为υ2,那么全程的平均速度是:( D )
A、(υ1+υ2)/2
B、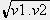

C、(υ21+υ22)/(υ1+υ2)
D、2υ1υ2/(υ1+υ2)
例2、甲向南走100米的同时,乙从同一地点出发向东也行走100米,若以乙为参照物,求甲的位移大小和方向?(100(2)1/2米;东偏北450)

例3、某人划船逆流而上,当船经过一桥时,船上一小木块掉在河水里,但一直航行至上游某处时此人才发现,便立即返航追赶,当他返航经过1小时追上小木块时,发现小木块距离桥有6000米远,若此人向上和向下航行时船在静水中前进速率相等。试求河水的流速为多大?
6、加速度:描述物体速度变化快慢的物理量,a=△υ/△t (又叫速度的变化率)是矢量。a的方向只与△υ的方向相同(即与合外力方向相同)
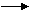
 a方向 υ方向相同时 作加速运动;
a方向 υ方向相同时 作加速运动;
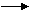 a方向 υ方向相反时 作减速运动;
a方向 υ方向相反时 作减速运动;
加速度的增大或减小只表示速度变化快慢程度增大或减小,不表示速度增大或减小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com