
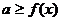 有解
有解 的最小值;
的最小值; 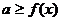 无解
无解 的最小值;
的最小值;
★★★ 突 破 重 难 点
【范例1】已知f(x)=3x-b(2≤x≤4,b为常数)的图象经过点(2,1),求F(x)=[f-1(x)]2-f-1(x2)的值域。
分析提示:求函数值域时,不但要重视对应法则的作用,而且要特别注意定义域的制约作用。本题要注意F(x)的定义域与f-1(x)定义域的联系与区别。
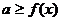 恒成立
恒成立 的最大值;
的最大值;
 恒成立
恒成立 的最小值;
的最小值;
数形结合:要注意代数式的几何意义。如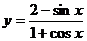 的值域。(几何意义??斜率)
的值域。(几何意义??斜率)
反之:方程有解也可转化为函数求值域。如方程 有解,求
有解,求 的范围。
的范围。
判别式:适合于可转化为关于 的一元二次方程的函数求值域。如
的一元二次方程的函数求值域。如 。
。
注意函数 的单调性。
的单调性。
基本不等式:要注意“一正、二定、三相等”,
单调性:特别适合于指、对数函数的复合函数。如求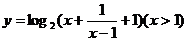 值域。
值域。
如求 的值域。
的值域。
反解法:有界量用 来表示。如
来表示。如 ,
, ,
, 等等。如,
等等。如, 。
。
换元法:通过变量代换转化为能求值域的函数,特别注意新变量的范围。注意三角换元的应用。
直观法:图象在 轴上的“投影”的范围就是值域的范围;
轴上的“投影”的范围就是值域的范围;
配方法:适合一元二次函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com