
试合格就签约;乙、丙则约定:如果两人面试都合格就一同签约,否则两人都不签约。设甲面试合格的概率为 ,乙、丙面试合格的概率都是
,乙、丙面试合格的概率都是 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率;
 (2)设
(2)设 ,证明:
,证明: 为常数.
为常数.
20(本小题满分13分)
甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约。甲表示只要面
(1)当直线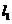 的倾斜角为
的倾斜角为 ,双曲线的焦距为8时,求椭圆的方程;
,双曲线的焦距为8时,求椭圆的方程;
已知椭圆 的方程为
的方程为 双曲线
双曲线 的两条渐近线为
的两条渐近线为 和
和 ,过椭圆
,过椭圆 的右焦点
的右焦点 作直线
作直线 ,使得
,使得 于点
于点 ,又
,又 与
与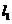 交于点
交于点 ,
, 与椭圆
与椭圆 的两个交点从上到下依次为
的两个交点从上到下依次为 (如图).
(如图).
 正四棱柱ABCD―A1B
正四棱柱ABCD―A1B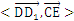 =
=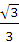 .
.
(1)建立适当的坐标系,求出E点的坐标;
(2)证明:EF是异面直线D1B与AD的公垂线;
(3)求二面角D1―BF―C的余弦值.
18(本小题满分12分)
某机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利总额为y万元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值)
(3)使用若干年后,对机床的处理方案有两种:(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.
19(本小题满分12分)
向量a=(sinωx+cosωx,1),b=(f(x),simωx),其中0<ω<l,且a∥b.将f(x)的图象沿x轴向左平移 个单位,沿y轴向下平移
个单位,沿y轴向下平移 个单位,得到g(x)的图象,已知g(x)的图象关于(
个单位,得到g(x)的图象,已知g(x)的图象关于( ,0)对称
,0)对称
(1)求ω的值;
(2)求g(x)在[0,4π]上的单调递增区间.
17(本小题满分12分)
15.甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头(假设无其它船驶向该码头),它们在一昼夜内任何时刻到达是等可能的.如果甲船和乙船的停泊时间都是4小时,则它们中的任何一条船不需要等等码头空出的概率为
16(本小题满分12分)
14.用4种不同的颜色为正方体A 的六个面着色,要求相邻两个面颜色不相同,则不同的着色方法种数有
的六个面着色,要求相邻两个面颜色不相同,则不同的着色方法种数有
13.一个总体共有100个个体,随机编号0,1,2,…,99,按从小到大的编号顺序平均分成10个小组,组号依次为1,2,3,…,10,现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=4,则在第6组中抽取的号码是
12.若直线 始终平分圆的周
始终平分圆的周 长,则
长,则 的最小值为
的最小值为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com