
E
A1 C1
D B1
①∵面A1EC⊥侧面AC1,
∴EG⊥侧面AC1;取AC中点F,连结BF,FG,由AB=BC得BF⊥AC,
②∵面ABC⊥侧面AC1,
∴BF⊥侧面AC1;得BF∥EG,BF、EG确定一个平面,交侧面AC1于FG。
③∵BE∥侧面AC1,
∴BE∥FG,四边形BEGF是平行四边形,BE=FG,
④∵BE∥AA1,
∴FG∥AA1,△AA1C∽△FGC,
⑤∵AF=FC,
∴FG=AA1=BB1,即BE=BB1,故BE=EB1。
(Ⅱ)解:分别延长CE、C1B1交于点D,连结A1D
∵EB1∥CC1,EB1=BB1=CC1,
∴DB1=DC1=B1C1=A1B1,
∵∠B1A1C1=∠B1C1A1=600,∠DA1B1=∠A1DB1=(1800-∠DB1A1)=300,
∴∠DA1C1=∠DA1B1+∠B1A1C1=900,即DA1⊥A1C1。
∵CC1⊥面A1C1B1,即A1C1是A1C在平面A1C1D上的射影,根据三垂线定理得DA1⊥A1C
所以∠CA1C1是所求二面角的平面角。
∵CC1=AA1=A1B1=A1C1,∠A1C1C=900,
∴∠CA1C1=450,即所求二面角为450。
(23)(本小题满分10分)
某地现有耕地10000公顷。规划10年后粮食单产比现在增加22%,人均粮食占有量比现在提高10%。如果人口年增长率为1%,那么耕地平均每年至多只能减少多少公顷(精确到1公顷)?
(=,=)
解:设耕地平均每年至多只能减少x公顷,又设该地区现有人口为P人,粮食单产为M吨/公顷。
依题意得不等式
化简得
答:按规划该地区耕地平均每年至多只能减少4公顷。
(24)(本小题满分12分)
已知是过点P()的两条互相垂直的直线,且与双曲线各有两交点,分别为A1、B1和A2、B2。
(Ⅰ)求的斜率k1的取值范围;
(Ⅱ)若|A1B1|=|A2B2|,求的方程。
解:(Ⅰ)依题意,的斜率都存在。因为过点P()且与双曲线有两个交点,故方程组
(1)
有两个不同的解。在方程组(1)中消去y,整理得
(2)
若,则方程组(1)只有一个解,即与双曲线只有一个交点,与题设矛盾。
故,即。方程(2)的判别式为
设的斜率为k2,因为过点P()且与双曲线有两个交点,故方程组
(3)
有两个不同的解。在方程组(3)中消去y,整理得
(4)
同理有,
又因为,所以有
于是,与双曲线各有两个交点,等价于
(Ⅱ)设A1(x1,y1)B1(x2,y2).由方程(2)知
同理,由方程(4)可求得|A2B2|2,整理得
由|A1B1|=|A2B2|,得|A1B1|2=5|A2B2|2.
将(5)、(6)代入上式得
解得
取时,
取时,
(25)(本小题满分12分)
已知是实数,函数当时,
(Ⅰ)证明:
(Ⅱ)证明:当时,
(Ⅲ)设当时,的最大值为2,求.
(Ⅰ)证明:由条件当时,,
取x=0得,即
(Ⅱ)证法一:当时,在[-1,1]上是增函数,
由此得
当时,在[-1,1]上是减函数,
由此得
当时,
综上得
证法二:由可得
当时,有
根据含绝对值的不等式的性质,得
即
(Ⅲ)因为时,在[-1,1]上是增函数,
当x=1时取最大值2,
即
因为当时,,即
根据二次函数的性质,直线x=0为的图象的对称轴,由此得
由(1)得
所以
一九九六年(文科)
(1)已知全集I={1,2,3,4,5,6,7}集合A={1,3,5,7},B={3,5}.则 ( C )
(A) (B) (C) (D)
(A) y (B) y (C) y (D) y
o 1 x o 1 x o 1 x o 1 x
(3)若,则x的取值范围是 ( D )
(A)
(B)
(C)
(D)
(4)复数等于 ( B )
(A) (B) (C) (D)
(5)6名同学排成一排,其中甲、乙两人必须排在一起的不同排法有 ( C )
(A)720种 (B)360种 (C)240种 (D)120种
(6)已知是第三象限角且,则 ( D )
(A) (B) (C) (D)
(7)如果直线、与平面、、满足:和,那么必有 ( A )
(A)且 (B)且
(C)且 (D)且
(8)当时,函数的 ( D )
(A)最大值是1,最小值是-1
(B)最大值是1,最小值是
(C)最大值是2,最小值是-2
(D)最大值是2,最小值是-1
(9)中心在原点,准线方程为,离心率为的椭圆方程是
(A) (B) ( A )
(C) (D)
(10)圆锥母线长为1,侧面展开图圆心角为2400,该圆锥的体积是 ( C )
(A) (B) (C) (D)
(11)椭圆的两个焦点坐标是 ( B )
(A)(-3,5),(-3,-5) (B)(3,3),(3,-5)
(C)(1,1),(-7,1) (D)(7,-1),(-1,-1)
(12)将边长为的正方形ABCD沿对角线AC折起,使得BD=,则三棱锥D-ABC的体积为 ( D )
(A) (B) (C) (D)
(13)等差数列的前m项和为30,前2m项和为100,则它的前3m项和为 ( C )
(A)130 (B)170 (C)210 (D)260
(14)设双曲线的半焦距为c,直线过(,0),(0,)两点。已知原点到直线的距离为,则双曲线的离心率为 ( A )
(A)2 (B) (C) (D)
(15)设是上的奇函数,,当时,,则等于 ( B )
(A)0.5 (B)-0.5 (C)1.5 (D)-1.5
(16)已知圆与抛物线的准线相切。则p=__________
答:2
(17)正六边形的中心和顶点共7个点,以其中3个点为顶点的三角形共有_______个(用数字作答)
答:32
(18)的值是_______
A B
F E
答:
(19)如图,正方形ABCD所在平面与正方形ABEF所在平面成600的二面角,则异面直线AD与BF所成角的余弦值是_______
答:
(20)(本小题满分11分)
解不等式
解:(Ⅰ)当时,原不等式等价于不等式组:
因为所以
(Ⅱ)当时,原不等式等价于不等式组:
由(1)得,
由(2)得,
综上,当时,不等式的解集为
当时,不等式的解集为
(21)(本小题满分12分)
已知△ABC的三个内角A,B,C满足:
A+C=2B,求的值。
解:由题设条件知:
B=600,A+C=1200
利用和差化积及积化和差公式,上式可化为
将代入上式并整理得
从而得
(22)(本小题满分12分)
如图,在正三棱柱ABC-A1B1C1中,E∈BB1,截面A1EC⊥侧面AC1
A C
B
E
A1 C1
B1
(Ⅰ)求证:BE=EB1;
(Ⅱ)若AA1=A1B1,求平面A1EC与平面A1B1C1所成二面角(锐角)的度数。
注意:在下面横线上填写适当内容,使之成为(Ⅰ)的完整证明,并解答(Ⅱ)。
(Ⅰ)证明:在截面A1EC内,
过E作EG⊥A1C,G是垂足。
A F C
B
由题设知xR,>0,x>0.
由点R在椭圆上及点O,Q,R共线,得方程组
解得
由点O,Q,P共线,得
即
由题设|OQ|?|OP|=|OR|2,得
将(1)、(2)(3)式代入上式,整理得点Q的轨迹方程
所以点Q的轨迹是以(1,0)为中心,长、短半轴分别为1和且长轴在x轴上的椭圆,去掉坐标原点。
一九九六年(理科)
(1)已知全集I=N,集合,。则 ( C )
(A) (B) (C) (D)
(A) y (B) y (C) y (D) y
o 1 x o 1 x o 1 x o 1 x
(3)若,则x的取值范围是 ( D )
(A)
(B)
(C)
(D)
(4)复数等于 ( B )
(A) (B) (C) (D)
(5)如果直线、与平面、、满足:和,那么必有 ( A )
(A)且 (B)且
(C)且 (D)且
(6)当时,函数的 ( D )
(A)最大值是1,最小值是-1
(B)最大值是1,最小值是
(C)最大值是2,最小值是-2
(D)最大值是2,最小值是-1
(7)椭圆的两个焦点坐标是 ( B )
(A)(-3,5),(-3,-3) (B)(3,3),(3,-5)
(C)(1,1),(-7,1) (D)(7,-1),(-1,-1)
(8)若,则等于 ( A )
(A) (B) (C) (D)
(9)将边长为的正方形ABCD沿对角线AC折起,使得BD=,则三棱锥D-ABC的体积为 ( D )
(A) (B) (C) (D)
(10)等比数列的首项,前n项和为,若,则等于 ( B )
(A) (B) (C)2 (D)-2
(11)椭圆的极坐标方程为,则它在短轴上的两个顶点的极坐标是 ( C )
(A)(3,0),(1,) (B)(),()
(C)(2,),(2,) (D)(),()
(12)等差数列的前m项和为30,前2m项和为100,则它的前3m项和为 ( C )
(A)130 (B)170 (C)210 (D)260
(13)设双曲线的半焦距为c,直线过(,0),(0,)两点。已知原点到直线的距离为,则双曲线的离心率为 ( A )
(A)2 (B) (C) (D)
(14)母线长为1的圆锥的体积最大时,其侧面展开图圆心角等于 ( D )
(A) (B) (C) (D)
(15)设是上的奇函数,,当时,,则等于 ( B )
D C
F
A B
E
(Ⅰ)证明:根据圆柱性质,
DA⊥平面ABE
∵BE平面ABE,
∴DA⊥EB.
∵AB是圆柱底面的直径,
点E在圆周上,
∴AE⊥EB,又AE∩AD=A,故得
EB⊥平面DAE∵AF平面DAE,∴EB⊥AF
又AF⊥DE,且EB∩DE=E,故得
AF⊥平面DEB.∵DB平面DEB
∴AF⊥DB.
(Ⅱ)解:设点E到平面ABCD的距离为d
记AD=h,因圆柱轴截面ABCD是矩形,所以AD⊥AB。
S△ABD=AB?AD=
VD-ABE=VE-ABD=S△ABD=
又V圆柱=π?AD=,
由题设知
即
(25)(本小题满分12分)
某地为促进淡水鱼养殖业的发展,将价格控制在适当范围内,决定对淡水鱼养殖提供政府补贴。设淡水鱼的市场价格为x元/千克,政府补贴为t元/千克,根据市场调查,当8≤x≤14时,淡水鱼的市场日供应量P千克与市场日需求量Q千克近似的满足关系:
当P=Q时的市场价格称为市场平衡价格。
(Ⅰ)将市场平衡价格表示为政府补贴的函数,并求出函数的定义域;
(Ⅱ)为使市场平衡价格不高于每千克10元,政府补贴至少为每千克多少元?
解:(Ⅰ)依题设有
化简得
当判别式时,可得
解不等式组①,得不等式组②无解。
故所求的函数关系式为
函数的定义域为[0,]
(Ⅱ)为使,应有
化简得
解得
从而政府补贴至少为每千克1元。
(26)(本小题满分12分)
已知椭圆,直线.P是上一点,射线OP交椭圆于点R,又点Q在OP上且满足|OQ|?|OP|=|OR|2.当点P在上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线。
解:由题设知点Q不在原点.设P,R,Q的坐标分别为
P
R
Q
O x
(12,yP),(xR,yR),(x,y),
所以原方程的解为x=2.
(22)(本小题满分12分)
设复数求复数的模和辐角。
解:
所以复数的模为;
辐角为
(23)(本小题满分10分)
设是由正数组成的等比数列,是其前n项和。
证明
证明:设的公比为,由题设知
(1)当时,从而
(2)当时,从而
由(1)和(2)得
根据对数函数的单调性,知
即
证法二:设的公比为,由题设知
即(以下同证法一)
(24)(本小题满分12分)
如图,ABCD是圆柱的轴截面,点E在底面的圆周上,AF⊥DE,F是垂足。
(Ⅰ)求证:AF⊥DB;
(Ⅱ)如果AB=,圆柱与三棱锥D-ABE的体积比等于,求点E到截面ABCD的距离。
(20)四个不同的小球放入编号为1、2、3、4的四个盒中,则恰有一个空盒的放法共有________种(用数字作答)
答:144
(21)(本小题满分7分)
解方程
解:设,则原方程可化为
(20)四个不同的小球放入编号为1、2、3、4的四个盒中,则恰有一个空盒的放法共有________种(用数字作答)
答:144
(21)(本小题满分7分)
在复平面上,一个正方形的四顶点按照逆时针方向依次为Z1,Z2,Z3,O(其中O是原点),已知Z2对应复数。求Z1和Z3对应的复数。
解:设Z1,Z3对应的复数分别为
依题设得
(22)(本小题满分10分)
求的值。
解:原式=
(23)(本小题满分12分)
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足。
(Ⅰ)求证:AF⊥DB;
(Ⅱ)如果圆柱与三棱锥D-ABE的体积比等于,求直线DE与平面ABCD所成的角。
D C
F
A H B
E
(Ⅰ)证明:根据圆柱性质,
DA⊥平面ABE
∵BE平面ABE,
∴DA⊥EB.
∵AB是圆柱底面的直径,
点E在圆周上,
∴AE⊥EB,又AE∩AD=A,故得
EB⊥平面DAE∵AF平面DAE,∴EB⊥AF
又AF⊥DE,且EB∩DE=E,故得
AF⊥平面DEB.∵DB平面DEB
∴AF⊥DB.
(Ⅱ)解:过点E作EH⊥AB,H是垂足,连结DH.
根据圆柱性质,平面ABCD⊥平面ABE,AB是交线,且EH平面ABE,
∴EH⊥平面ABCD.
又DH平面ABCD,∴DH是ED在平面ABCD上的射影,
从而∠EDH是DE与平面ABCD所成的角.
设圆柱的底面半径而R,则DA=AB=2R,于是V圆柱=2πR3,
VD-ABE=AD?S△ABE=?EH.
V圆柱:VD-ABE=3π,得EH=R.
可知H是圆柱底面的圆心,AH=R,
DH=
∴∠EDH=
(24)(本小题满分12分)
某地为促进淡水鱼养殖业的发展,将价格控制在适当范围内,决定对淡水鱼养殖提供政府补贴。设淡水鱼的市场价格为x元/千克,政府补贴为t元/千克,根据市场调查,当8≤x≤14时,淡水鱼的市场日供应量P千克与市场日需求量Q千克近似的满足关系:
当P=Q时的市场价格称为市场平衡价格。
(Ⅰ)将市场平衡价格表示为政府补贴的函数,并求出函数的定义域;
(Ⅱ)为使市场平衡价格不高于每千克10元,政府补贴至少为每千克多少元?
解:(Ⅰ)依题设有
化简得
当判别式时,可得
解不等式组①,得不等式组②无解。
故所求的函数关系式为
函数的定义域为[0,]
(Ⅱ)为使,应有
化简得
解得
从而政府补贴至少为每千克1元。
(25)(本小题满分12分)
设是由正数组成的等比数列,是其前n项和。
(Ⅰ)证明
(Ⅱ)是否存在常数c>0使得
成立?并证明你的结论。
(Ⅰ)证明:设的公比为,由题设知
(1)当时,从而
(2)当时,从而
由(1)和(2)得
根据对数函数的单调性,知
即
(Ⅱ)解:要使
成立,则有
分两种情况讨论:(1)当时,
可知,不满足条件①,即不存在常数c>0,使结论成立。
(2)当时,若条件①成立,因
且故只能有即
此时,
但时,不满足条件②,
即不存在常数c>0,使结论成立。
证法二:用反证法.假设存在常数c>0,使
,
则有
由(4)得
根据平均值不等式及(1)、(2)、(3)、(4)知
因为c>0,故(5)式右端非负,而由(Ⅰ)知,(5)式左端小于零,矛盾。
故不存在常数c>0,使
(26)(本小题满分12分)
已知椭圆,直线.P是上一点,射线OP交椭圆于点R,又点Q在OP上且满足|OQ|?|OP|=|OR|2.当点P在上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线。
解:由题设知点Q不在原点.设P,R,Q的坐标分别为
y
P
Q R
O x
(xP,yP),(xR,yR),(x,y),
其中x,y不同时为零.
当点P不在y轴上时,
由于点R在椭圆上及点O,
Q,R共线,得方程组
解得
由于点P在直线上及点O,Q,P共线,
解方程组
解得
当点P在y轴上时,经检验(1)~(4)式也成立
由题设|OQ|?|OP|=|OR|2,得
将(1)~(4)式代入上式,化简整理得
因x与xP同号或y与yP同号,以及(3),(4)知,
故点Q的轨迹方程为
所以点Q的轨迹是以(1,1)为中心,长、短半轴分别为和且长轴与x轴平行的椭圆,去掉坐标原点。
解法二:由题设点Q不在原点.又设P,R,Q的坐标分别为
(xP,yP),(xR,yR),(x,y),其中x,y不同时为零.
设OP与x轴正方向的夹角为,则有
由上式及题设|OQ|?|OP|=|OR|2,得
由点P在直线上,点R在椭圆上,得方程组
将(1),(2),(3),(4)代入(5),(6),
整理得点Q的轨迹方程为
所以点Q的轨迹是以(1,1)为中心,长、短半轴分别为和且长轴与x轴平行的椭圆,去掉坐标原点。
解法三:投影法
设P,R,Q的坐标分别为(xP,yP),(xR,yR),(x,y),其中x,y不同时为零.
由题设|OQ|?|OP|=|OR|2
设OP的方程为
这就是Q点的参数方程,消去参数k得
当P在y轴上时,k不存在,此时Q(0,2)满足方程,
故Q点轨迹是以(1,1)为中心,长、短半轴分别为和且长轴与x轴平行的椭圆,去掉坐标原点。
解法四:极坐标法
在极坐标系OX中,设∠POX=
由得
由得
由|OQ|?|OP|=|OR|2得即
将(1),(2)代入(3)
故Q点轨迹是以(1,1)为中心,长、短半轴分别为和且长轴与x轴平行的椭圆,去掉坐标原点。
一九九五年(文科)
(1)已知全集I={0,-1,-2,-3,-4,}集合M={0,-1,-2},N={0,-3,-4},则 ( B )
o 1 x -1 o x o 1 x -1 o x
(A){0} (B){-3,-4} (C){-1,-2} (D)
(2)函数的图象是 ( D )
(3)函数的最小正周期是 ( C )
(A) (B) (C) (D)
(4)正方体的全面积是,它的顶点都在球面上,这个球的表面积是 ( B )
(A) (B) (C) (D)
(5)若图中的直线的斜率分别为,则 ( D )
O
x
(A)
(B)
(C)
(D)
(6)双曲线的渐近线方程是 ( C )
(A) (B) (C) (D)
(7)使成立的的取值范围是 ( A )
(A) (B) (C) (D)
(8)圆的位置关系是 ( C )
(A)相离 (B)外切 (C)相交 (D)内切
(9)已知是第三象限角,且,那么等于
(A) (B) (C) (D)( A )
(10)如图,ABCD-A1B1C1D1是正方体,
D1 F1 C1
A1 E1 B1
D C
A B
B1E1=D1F1=,则BE1与DF1所成角
的余弦值是 ( A )
(A) (B)
(C) (D)
(11)已知是x的减函数,则的取值范围是( B )
(A)(0,2) (B)(0,1) (C)(1,2) (D)(2,+)
(12)在的展开式中,的系数是 ( D )
(A)-297 (B)-252 (C)297 (D)207
(13)已知直线,直线.有下面四个命题:( D )
① ②
③ ④
其中正确的两个命题是
(A)①与② (B)③与④ (C)②与④ (D)①与③
(14)等差数列的前n项和分别为与,若
等于 ( C )
(A)1 (B) (C) (D)
(15)用1,2,3,4,5这五个数字,组成没有重复数字的三位数,其中偶数共有 ( A )
(A)24个 (B)30个 (C)40个 (D)60个
(16)方程的解是__________
答:3
(17)已知圆台上、下底面圆周都在球面上,且下底面过球心,母线与底面所成的角为,则圆台的体积与球体积之比_______
答:
(18)函数的最大值是_______
答:
(19)直线过抛物线的焦点,并且与x轴垂直,则被抛物线截得的线段长为_______
答:4
(I)设n年内(本年度为第一年)总投入为 万元,旅游业的总收入为
万元,旅游业的总收入为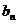 万元。写出
万元。写出 、
、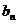 的表达式;
的表达式;
(II)至少经过几年旅游业的总收入才能超过总投入?(01-21-12分)
8、从社会效益和经济效益出发,某地投入资金进行生态环境建设, 并以此发展旅游产业。根据规划,本年度投入800万元,以后每年投入比上年减少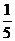 。本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
。本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加 。
。
(Ⅱ)为使本年度的年利润比上年有所增加,问投入成本增加的比例 应在什么范围内?(01春-21-12分)
应在什么范围内?(01春-21-12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com