
(1)若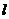 与
与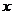 轴交于点
轴交于点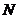 ,且
,且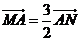 ,求直线
,求直线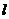 的方程;
的方程;
20.(本题13分)已知椭圆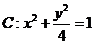 ,过点
,过点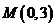 的直线
的直线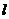 与椭圆
与椭圆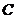 相交于不同的两点
相交于不同的两点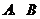 .
.
(2)若某个人连续操作四次(每次操作后把球放回),问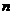 为何值时,他“获胜”的概率最大?
为何值时,他“获胜”的概率最大?
(1)若游戏参与者只有一次操作的机会,他“获胜”的概率为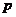 .试用
.试用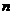 表示
表示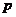 ,并求
,并求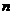 为何值时,
为何值时,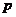 最大?
最大?
19.(本题12分)有一种游戏,要求游戏者从一个不透明的箱子中摸球,箱子中装有6个不同编号的白球和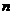 个
个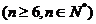 不同编号的黄球(这些球外形相同),操作一次就是从中摸出两球,若摸出的两球颜色不同,该次操作得
不同编号的黄球(这些球外形相同),操作一次就是从中摸出两球,若摸出的两球颜色不同,该次操作得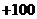 分;若摸出的两球颜色相同,该次操作得
分;若摸出的两球颜色相同,该次操作得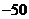 分.一个人操作若干次,如果总得分恰为
分.一个人操作若干次,如果总得分恰为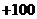 分,就称游戏“获胜”.
分,就称游戏“获胜”.
(2)若不等式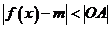 (O为原点)在
(O为原点)在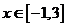 上恒成立,求实数的
上恒成立,求实数的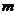 的取值范围.
的取值范围.
(1)求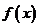 的单调区间;
的单调区间;
18.(本题12分)已知函数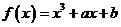 在点
在点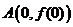 处的切线方程为
处的切线方程为 .
.
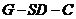 的大小为
的大小为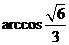 ?若存在,求出
?若存在,求出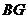 的长;若不存在,说明理由.
的长;若不存在,说明理由.
(3)在线段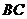 上是否存在一点
上是否存在一点 ,使二面角
,使二面角
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com