
23.如图11-1,小明在研究正方形ABCD的有关问题时,得出:“在正方形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE =∠EAD,那么EF⊥AE”.他又将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图11-2、11-3、图11-4),其他条件不变,发现仍然有“EF⊥AE”的结论.
你同意小明的观点吗?若同意,请结合图11-4加以证明;若不同意,请说明理由.
22.某班级为准备元旦联欢会,欲购买价格分别为2元、4元和10元的三种奖品,每种奖品至少购买一件,共买16件,恰好用50元.若2元的奖品购买a件.
⑴用含a的代数式表示另外两种奖品的件数;
⑵请你设计购买方案,并说明理由.
21. 星期天,小强骑自行车到郊外与同学一起游玩.从家出发2小时到达目的地,游玩3小时后按原路以原速返回,小强离家4小时40分钟后,妈妈驾车沿相同路线迎接小强,图10是他们离家的路程y(千米)与时间x(时)的函数图象.已知小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时.
⑴小强家与游玩地的距离是多少?
⑵妈妈出发多长时间与小强相遇?
20.为丰富学生的校园文化生活,振兴中学举办了一次学生才艺比赛,三个年级都有男、女各一名选手进入决赛.初一年级选手编号为男1号、女1号,初二年级选手编号为男2号、女2号,初三年级选手编号为男3号、女3号.比赛规则是男、女各一名选手组成搭档展示才艺.
⑴用列举法说明所有可能出现搭档的结果;
⑵求同一年级男、女选手组成搭档的概率;
⑶求高年级男选手与低年级女选手组成搭档的概率.
19.如图9,在直角坐标系中,图形①与图形②关于点P成中心对称.
⑴画出对称中心P,并写出点P的坐标;
⑵将图形②向下平移4个单位,画出平移后的图形③,并判断图形③与图形①的位置关系.(直接写出结果)
18.某学校为丰富大课间自由活动的内容,随机选取本校100名学生进行调查,调查内容是“你最喜欢的自由活动项目是什么”,整理收集到的数据,绘制成图8.
⑴学校采用的调查方式是______________________;
⑵求喜欢“踢毽子”的学生人数,并中图8中将“踢毽子”部分的图形补充完整;
⑶该校共有800名学生,请估计喜欢“跳绳”的学生人数.
17.解方程: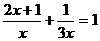
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com