
(4)如图②,连接 ,并把
,并把 沿
沿 翻折,得到四边形
翻折,得到四边形 ,那么是否存在某一时刻
,那么是否存在某一时刻 ,使四边形
,使四边形 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
(3)是否存在某一时刻 ,使线段
,使线段 恰好把
恰好把 的周长和面积同时平分?若存在,求出此时
的周长和面积同时平分?若存在,求出此时 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(2)设 的面积为
的面积为 (
( ),求
),求 与
与 之间的函数关系式;
之间的函数关系式;
(1)当 为何值时,
为何值时,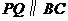 ?
?
已知:如图①,在 中,
中, ,
, ,
, ,点
,点 由
由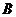 出发沿
出发沿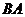 方向向点
方向向点 匀速运动,速度为1cm/s;点
匀速运动,速度为1cm/s;点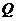 由
由 出发沿
出发沿 方向向点
方向向点 匀速运动,速度为2cm/s;连接
匀速运动,速度为2cm/s;连接 .若设运动的时间为
.若设运动的时间为 (
( ),解答下列问题:
),解答下列问题:
24.(本小题满分12分)
(2)若要确保摸出的小球至少有 个同色(
个同色( ),则最少需摸出小球的个数是 .
),则最少需摸出小球的个数是 .
问题解决:(1)请把本题中的“实际问题”转化为一个从口袋中摸球的数学模型;
(2)根据(1)中建立的数学模型,求出全校最少需抽取多少名学生.
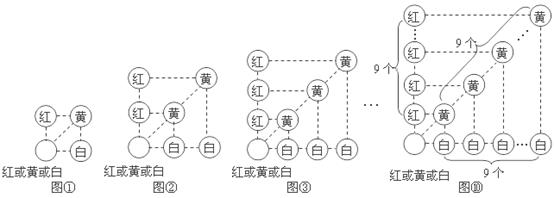
模型拓展二:在不透明口袋中装有 种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 .
(3)若要确保摸出的小球至少有 个同色(
个同色( ),则最少需摸出小球的个数是 .
),则最少需摸出小球的个数是 .
模型拓展一:在不透明的口袋中装有红、黄、白、蓝、绿五种颜色的小球各20分(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 ;
(2)若要确保摸出的小球至少有10个同色,则最少需摸出小球的个数是 ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com