1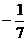．的绝对值是

（3）在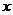轴的上方是否存在点P、点Q，使以点O、B、P、Q为顶点的平行四边形的面积是矩形ABOC面积的2倍，且点P在抛物线上，若存在，请求出点P、点Q的坐标；若不存在，请说明理由。

（1）判断点E是否在轴上，并说明理由；

（2）求抛物线的函数表达式；

26．如下图所示，在平面直角坐标系中，矩形ABOC的边BO在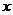轴的负半轴上，边OC在轴的正半轴上，且AB=1，OB=，矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD。点A的对应点为点E，点B的对应点为点F，点C的对应点为点D，抛物线过点A、E、D。

（1）求证：①BE=CD；②△AMN是等腰三角形。

（2）在图甲的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图乙所示的图形。请直接写出（1）中的两个结论是否仍然成立；

（3）在（2）的条件下，请你在图乙中延长ED交线段BC于点P。求证：△PBD∽△AMN。

八、（本题14分）

25．已知：如下图甲所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B、A、D在一条直线上，连结BE、CD，M、N分别为BE、CD的中点。

（2）按照（1）中的变化规律，货车从A处出发行驶4.2小时到达C处，求此时油箱内余油多少升？

（3）在（2）的前提下，C处前方18千米的D处有一加油站，根据实际经验此货车在行驶中油箱内至少保证有10升油，如果货车的速度和每小时的耗油量不变，那么在D处至少加多少升油，才能使货车到达B地。（货车在D处加油过程中的时间和路程忽略不计）

七、（本题12分）

（1）请你认真分析上表中所给的数据，用你学过的一次函数、反比例函数和二次函数中的一种来表示与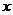之间的变化规律，说明选择这种函数的理由，并求出它的函数表达式；（不要求写出自变量的取值范围）

余油量（升）

100

80

60

50