
2.计算 的结果是( )
的结果是( )
1.若 ,则
,则 的平方根是( )
的平方根是( )
A.16 B.±
7.如图:某海域内有三个港口 A、D、C,港口C在港口A北偏东600 方向上,港口D在港口A北偏西600 方向上,一船以每小时25海里的速度沿北偏东300的方向驶离A港口,3小时候到达B点位置处,此时发现船舱漏水,海水以每小时48吨的速度渗入船内,当船舱渗入的海水总量超过75吨时,船将沉入海中,同时在B处测得港口C在B处的南偏东750方向上,若穿上的抽水机每小时可将8吨的海水排除船外,问此船在B处至少应以怎样的航行速度驶向最近的港口停靠才能保证船在抵达港口前不会沉没(计算结果保留根号)并指出此时船的航向(14分)
6.已知:如图:在△ABC和△ADE中 AB=AC AD=AE ∠BAC=∠DAE且点B、A、D在同一条直线上连接BE 、CD、M 、N 分别是BE 、CD的中点
(1)求证:BE=CD △AMN是等腰三角形
(2)在图1的基础上将△ADE绕点A按顺时针方向旋转1800,其它条件不变得到图2请直接写出(1)中的两个结论是否依然成立
(3)在(2)的条件下在图2中延长ED交线段BC于点P,求证:△PBD∽△AMN
(14分)
5.在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,顶点C在y轴的负半轴上,tan∠ABC=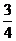 ,点P在线段OC上,且PO、PC的长(PO<
PC)是方程
,点P在线段OC上,且PO、PC的长(PO<
PC)是方程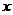 2-12
2-12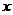 +27=0的根
+27=0的根
(1)求点P的坐标
(2)求AP的长
(3)在x轴上是否存在点Q,使点A、C、P、Q为顶点的四边形是梯形?若存在,请直接写出直线PQ的解析式,若不存在,说明理由(12分)
4.在Rt△ABC中
∠C=900,斜边C=5,两直角边长a、b是关于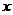 的一元二次方程
的一元二次方程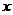 2-m
2-m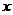 +
+
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com