
28.如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点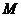 从
从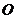 出发以每秒2个单位长度的速度向
出发以每秒2个单位长度的速度向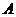 运动;点
运动;点 从
从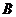 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向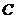 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点 作
作 垂直
垂直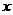 轴,垂足为
轴,垂足为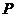 ,连结AC交NP于Q,连结MQ.
,连结AC交NP于Q,连结MQ.
(1)点______(填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,说明理由.
(2)若按关系式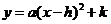 (
(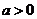 )将数据进行变换,请写出一个满足上述要求的这种关系式.并利用函数性质说明你所写函数关系式满足上述要求.
)将数据进行变换,请写出一个满足上述要求的这种关系式.并利用函数性质说明你所写函数关系式满足上述要求.
八、(本题11分)
(1)若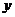 与
与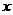 的关系式是
的关系式是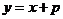
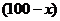 ,请说明:当
,请说明:当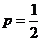 时,这种变换满足上述两个要求;
时,这种变换满足上述两个要求;
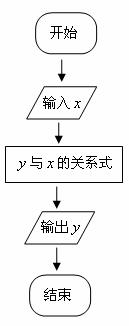
(i)新数据都在60~100(含60和100)之间;
(ii)新数据之间的大小关系与对应的原数据之间的大小关系一致,即原数据大的对应的新数据也较大.
27.按下图所示的流程,输入一个数据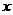 ,根据
,根据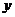 与
与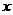 的关系式就输出一个数据
的关系式就输出一个数据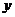 ,这样可以将一组数据变换成另一组新的数据.要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
,这样可以将一组数据变换成另一组新的数据.要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
七、(本题8分)
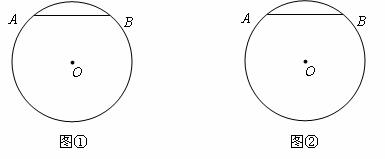
26.我们知道,用一块直角三角板就可以过一点画一条直线的垂线.
如图,AB是⊙O的弦,现在只有一块无刻度单位的直角三角板(斜边大于⊙O的直径),请你用两种不同的方法分别在图①、图②中确定出弦AB中点的位置(画出图形,标出直角),并且分别写出画图的步骤(不要证明).

六、(8分)
25.如下图,某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点有人求救,便立即派三名救生员前去营救。1号救生员从A点直接跳入海中;2号救生员沿岸边(岸边看成是直线)向前跑到C点,再跳入海中;3号救生员沿岸边向前跑300m到离B点最近的D点,再跳入海中.救生员在岸上跑的速度都是6m/s,在水中游泳的速度都是2m/s.若∠BAD= 45°,∠BCD=60°,三名救生员同时从A点出发,请说明谁先到达营救地点B. (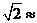 1.4,
1.4,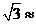 1.7)
1.7)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com