如图，已知抛物线y=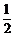x²?2x＋1的顶点为P，A为抛物线与y轴的交点，过A与y轴垂直的直线与抛物线的另一交点为B，与抛物线对称轴交于点O′，过点B和P的直线l交y轴于点C，连结O′C，将△ACO′沿O′C翻折后，点A落在点D的位置．

（1） （3分） 求直线l的函数解析式；

（2） （3分） 求点D的坐标；

（3） （3分） 抛物线上是否存在点Q，使得S_△DQC= S_△DPB? 若存在，求出所有符合条件的点Q的坐标；若不存在，请说明理由．

25．（本小题满分9分）

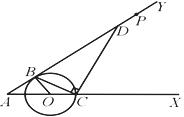
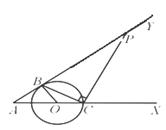
                                          图1                                    图2

（2）（6分）若P是AY上一点，AP=4，且sinA=，

① 如图2，当点D与点P重合时，求R的值；

② 当点D与点P不重合时，试求PD的长（用R表示）．

24．（本小题满分9分）

如图1，已知O是锐角∠XAY的边AX上的动点，以点O为圆心、R为半径的圆与射线AY切于点B，交射线OX于点C．连结BC，作CD⊥BC，交AY于点D．

（1）（3分）求证：△ABC∽△ACD；

23．（本小题满分8分）

如图，已知四边形ABCD、AEFG均为正方形，∠BAG=α （0°<α<180°）．

（1）（6分） 求证：BE=DG，且 BE⊥DG；

（2）（2分） 设正方形ABCD、AEFG的边长分别是3和2，线段BD、DE、EG、GB所围成封闭图形的面积为S．当α变化时，指出S的最大值及相应的α值．（直接写出结果，不必说明理由）

已知关于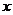的一元二次方程x²+kx?3=0，

（1）（4分） 求证：不论k为何实数，方程总有两个不相等的实数根；

（2）（4分） 当k=2时，用配方法解此一元二次方程．

22．（本小题满分8分）