①求平均每只玩具所需的生产费用为多少元．（用含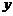的代数式表示）（生产费用=固定费用+材料费）

（1）求年产量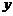（万只）与改造经费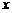（万元）之间的函数解析式。（不要求写出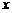的取值范围）

（2）已知每生产1万只玩具所需要的材料费是8万元．除材料费外，今年在生产中，全年还需支付出2万元的固定费用．

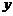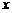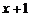25．（本小题满分10分）某小型玩具厂今年准备投入一定的经费用于现有生产设备的改造以提高经济效益．通过测算：今年玩具的年产量（万只）与投入的改造经费（万元）之间满足与成反比例，且当改造经费投入1万元时，今年的年产量是2万只．

24．（本小题满分9分）在正方形ABCD中，点E是AD上一动点，MN⊥AB分别交AB、CD于M、N．连结BE交MN于点O，过O作OP⊥BE分别交AB、CD于P、Q．

探究下列问题：

（1）如图（1），当点E在边AD上时，请你动手测量三条线段AE、MP、NQ的长度，并猜想AE与MP+NQ之间的数量关系，将结论直接写出；

（2）如图（2），若点E在边DA的延长线上时，AE、MP、NQ之间的数量关系又是怎样?并证明你所猜想的结论；

（3）如图（3），连结并延长BN交AD的延长线DG于H，若点E分别在线段DH和射线HG上时，判断AE、MP、NQ之间的数量关系，请直接写出结论．

联想拓展：

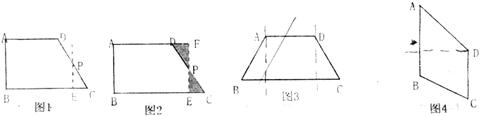
小明通过探究后发现：在一个四边形中，只要有一组对边平行，就可以剪拼成平行四边形．如图5的凸多边形中，AE=CD，AE∥CD，能否象上面剪切方法一样沿一条直线进行剪切，拼成一个平行四边形?若能，请你在图中画出剪拼的示意图并作必要的文字说明；若不能，简要说明理由．

23．（本小题满分9分）如图1，在直角梯形ABCD中，AD∥BC，∠B=∠A=90°，AD=a，BC=b，AB=c，

示例操作：

我们可以取直角梯形ABCD的非直角腰CD的中点P，过点P作PE∥AB，裁掉△PEC，并将△PEC拼接到△PFD的位置，构成新的图形（如图2）．

思考发现

小明在操作后发现，该剪拼方法就是先将△PEC绕点P逆时针旋转180°到△PFD的位置，易知PE与PF在同一条直线上。又因为在梯形ABCD中，AD∥BC，∠C+∠ADP=180°，则∠FDP+∠ADP=180°，所以AD和DF在同一条直线上。那么构成的新图形是一个四边形，进而根据平行四边形的判定方法，可以判断出四边形ABEF是一个平行四边形，而且还是一个特殊的平行四边形――矩形．

实践探究：

（1）矩形ABEF的面积是________；（用含a，b，c的式子表示）

（2）类比图2的剪拼方法，请你就图3和图4的两种情形分别画出剪拼成一个平行四边形的示意图．

22．（本小题满分8分）教师告诉同学们，可以用已知半径的球去测量圆柱形管子的内径，李明回家后把半径为5cm的小皮球置于保温杯的杯口上，经过思考找到了测量方法，问保温杯的内径是多少?