27．（本题12分）定义：到凸四边形一组对边距离相等，到另一组对边距离也相等的点叫凸四边形的准内点．如图1，PH＝PJ，PI＝PG，，则点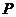就是四边形ABCD的准内点．

（1）如图2，∠AFD与∠DEC的角平分线FP，EP相交于点P．

求证：点P是四边形ABCD的准内点．

（2）分别画出图3平行四边形和图4梯形的准内点．（作图工具不限，不写作法，但要有必要的说明）

（3）判断下列命题的真假，在括号内填“真”或“假”。

①任意凸四边形一定存在准内点．（      ）

②任意凸四边形一定只有一个准内点．（      ）

③若P是任意凸四边形ABCD的准内点，则PA＋PB＝PC＋PD或PA＋PC＝PB＋PD．（      ）

26．（本题10分）如图所示，在直角坐标系xOy中，一次函数y₁＝k₁x＋b （k≠0）的图象与反比例函数（x＞0）的图象交于A（1，4），B（3，m）两点．

（1）试确定上述反比例函数和一次函数的表达式；

（2）在第一象限内， x取何值时，一次函数的函数值大于反比例函数的函数值；

（3）求△AOB的面积．

25．（本题8分）如图，等腰三角形ABC中，AB＝AC，D为CB延长线上一点，E为BC延长线上一点，且满足AB²＝DB?CE．

（1）说明：△ADB∽△EAC；

（2）若∠BAC＝40°，求∠DAE的度数．

24．（本题8分）有一枚均匀的正四面体，四个面上分别标有数字l，2，3，4，小红随机地抛掷一次，把着地一面的数字记为x；另有三张背面完全相同，正面上分别写有数字－2，－l，1的卡片，小亮将其混合后，正面朝下放置在桌面上，并从中随机地抽取一张，把卡片正面上的数字记为y；然后他们计算出S＝x＋y的值．

（1）用树状图或列表法表示出S的所有可能情况；

（2）分别求出当S＝0和S＜2时的概率．

23．（本题8分）已知：如图，四边形ABCD是菱形，过AB的中点E作AC的垂线EF，交AD于点M，交CD的延长线于点F．

（1）说明：AM＝DM；

（2）若DF＝2，求菱形ABCD的周长．

22．（本题8分）小玲用下面的方法来测量学校教学楼AB的高度：如图，在水平地面上放一面平面镜，镜子与教学楼的距离EA＝21米。当她与镜子的距离CE＝2．5米时，她刚好能从镜子中看到教学楼的顶端B。已知她的眼睛距地面高度DC＝1．6米．请你帮助小玲计算出教学楼的高度AB是多少米？（要求：精确到0．1米，提示：根据光的反射定律：反射角等于入射角）