（3）如图（3），△DEF的D点固定在AB的中点，然后绕D点按顺时针方向旋转△DEF， 使DF落在AB边上，此时F点恰好与B点重合，连接AE，请你求出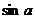的值。

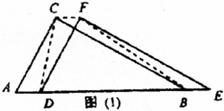
（2）如图（2），当D点移到AB的中点时，请你猜想四边形CDBF的形状，并说明理由。

25．（本小题满分10分）两个全等的直角三角形ABC和DEF重叠在一起，其中∠A＝60°，AC＝1。固定△ABC不动，将△DEF进行如下操作：

（1）如上图（1），△DEF沿线段AB向右平移（即D点在线段AB内移动），连接DC、CF、FB，四边形CDBF的形状在不断的变化，但它的面积不变化，请求出其面积。

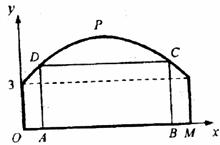
（1）直接写出点M及抛物线顶点P的坐标；

（2）求出这条抛物线的函数解析式；

（3）若变搭建一个矩形“支撑架”AD―DC―CB，使C、D点在抛物线上，A、B点在地面OM上，则这个“支撑架”总长的最大值是多少?

24．（本小题满分10分）如下图，某隧道横截面的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成，最大高度为6米，底部宽度为12米。现以O点为原点，OM所在直线为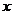轴建立直角坐标系。

（3）若△OAB绕点O按逆时针方向旋转30°，此时点B恰好落在反比例函数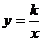的图像上，求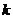的值。

（2）若将△OAB沿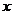轴向右平移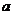个单位，此时点A恰好落在反比例函数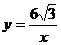的图像上，求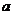的值；

（1）若△OAB关于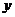轴的轴对称图形是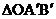，请直接写出A、B的对称点 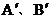的坐标；