1．下列各式从左到右的变形，是因式分解的是（    ）

　　（1）求这条抛物线的解析式；

　　（2）P为线段BM上一点，过点P向x轴引垂线，垂足为Q．若点P在线段BM上运动（点P不与点B、M重合），设OQ的长为t，四边形PQAC的面积为S．求S与t之间的函数关系式及自变量t的取值范围；

　　（3）在线段BM上是否存在点N，使△NMC为等腰三角形？若存在，请求出点N的坐标；若不存在，请说明理由。

29．如图，抛物线y＝ax²＋bx＋c与x轴交于A、B两点（点A在点B左侧），与y轴交于点C，且当x＝0和x＝2时，y的值相等。直线y＝3x - 7与这条抛物线相交于两点，其中一点的横坐标是4，另一点是这条抛物线的顶点M．

　　求证：（1） AB＝BH；

　　       （2） AB²＝GA?HE．

28．已知：如图，□ABCD中，∠DBC＝45°，DE⊥BC于E，BF⊥CD于F，DE、BF相交于H，BF、AD的延长线相交于G．

27．某超市为了吸引顾客，规定：凡购买50元以上的物品的顾客均可获奖，可以直接获得购物券5元，也可以参加摸奖。摸奖的方法是：从一个装有50个彩球的盒子中任取一球，摸到红球可获50元的购物券；摸到黄、篮球，可分别获30，10元的购物券，而摸到白球，不能获奖。已知50个球中，3个红球，5个黄球，10个篮球，其余均为白球。现有一位顾客决定参加摸奖，你认为他这种选择合算吗？为什么？

五、解答题（每小题10分，共30分）

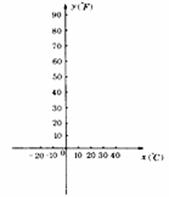
26．对于气温，通常有摄氏温度和华氏温度两种表示，且两者之间存在着某种函数关系，下列给出了摄氏（℃）温度x与华氏（°F）温度y之间对应关系．

x（℃）

…

－10

0

10

20

30

…

y（°F）

…

14

32

50

68

86

…

（1）通过①描点、连线；②猜想；③求解；④验证等几个步骤，试确定y与x之间的函数关系式；

（2）某天，沈阳的最高气温是12℃，台湾台北的最高气温是88°F，问这一天台北的最高气温比沈阳的最高气温高多少摄氏度（结果保留整数）？

25．已知正比例函数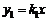和反比例函数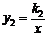的图像的一个交点为A（2，－1），求这两个函数的解析式。并求它们的另一个交点B的坐标。

7.5

　　（2）请从下列四个不同的角度对这次测试结果进行分析：

　　   ①从平均数和方差相结合看（分析谁的成绩更稳定）；

　　   ②从平均数和中位数相结合看（分析谁的成绩更好些）；

　　   ③从平均数和命中9环及以上的次数相结合看（分析谁的成绩更好些）；

　　   ④从折线图上两人射击命中环数的走势看（分析谁更有潜力）．