

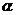 、
、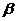 时(如图所示),物体B的运动速度
时(如图所示),物体B的运动速度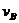 为(物体B不离开
为(物体B不离开
地面,绳始终有拉力)
A以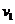 的速度向右匀速运动,当绳被拉成与水平面夹角分别是
的速度向右匀速运动,当绳被拉成与水平面夹角分别是
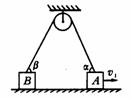 3.水平面上两物体A、B通过一根跨过定滑轮的轻绳相连,现物体
3.水平面上两物体A、B通过一根跨过定滑轮的轻绳相连,现物体
2.在地球的北极极点附近,地磁场可看做匀强磁场.假设一人站在北极极点,他面前有一根重
力不计的水平放置的直导线,通有方向自左向右的电流,则此导线受到的安培力方向是
A.向前 B.向后
C.向下 D.向上
 1.在固定于地面的斜面上垂直安放一个挡板,截面为 圆的柱状物体甲放在斜面上,半径与甲相等的光滑圆球乙被夹在甲与挡板之间,没有与斜面接触而处于静止状态,如图所示.现在从球心O1处对甲施加一平行于斜面向下的力F,使甲沿斜面方向极其缓慢地移动,直至甲与挡板接触为止.设乙对挡板的压力F1,甲对斜面的压力为F2,在此过程中
1.在固定于地面的斜面上垂直安放一个挡板,截面为 圆的柱状物体甲放在斜面上,半径与甲相等的光滑圆球乙被夹在甲与挡板之间,没有与斜面接触而处于静止状态,如图所示.现在从球心O1处对甲施加一平行于斜面向下的力F,使甲沿斜面方向极其缓慢地移动,直至甲与挡板接触为止.设乙对挡板的压力F1,甲对斜面的压力为F2,在此过程中
A.F1缓慢增大,F2缓慢增大
B.F1缓慢增大,F2缓慢减小
C.F1缓慢减小,F2缓慢增大
D.F1缓慢减小,F2不变
21.(本小题满分14分)
已知数列和满足:,其中为实数,为正整数.
(Ⅰ)对任意实数,证明数列不是等比数列;
(Ⅱ)试判断数列是否为等比数列,并证明你的结论;
(Ⅲ)设,为数列的前项和.是否存在实数,使得对任意正整数,都有
?若存在,求的取值范围;若不存在,说明理由.
解:本小题主要考查等比数列的定义、数列求和、不等式等基础知识和分类讨论的思想,考查综合分析问题的能力和推理认证能力,(满分14分)
(Ⅰ)证明:假设存在一个实数λ,使{an}是等比数列,则有a22=a1a3,即
矛盾.
所以{an}不是等比数列.
(Ⅱ)解:因为bn+1=(-1)n+1[an+1-3(n-1)+21]=(-1)n+1(an-2n+14)
=(-1)n?(an-3n+21)=-bn
又b1x-(λ+18),所以
当λ=-18,bn=0(n∈N+),此时{bn}不是等比数列:
当λ≠-18时,b1=(λ+18) ≠0,由上可知bn≠0,∴(n∈N+).
故当λ≠-18时,数列{bn}是以-(λ+18)为首项,-为公比的等比数列.
(Ⅲ)由(Ⅱ)知,当λ=-18,bn=0,Sn=0,不满足题目要求.
∴λ≠-18,故知bn= -(λ+18)?(-)n-1,于是可得
Sn=-
要使a<Sn<b对任意正整数n成立,
即a<-(λ+18)?[1-(-)n]〈b(n∈N+)
①
当n为正奇数时,1<f(n)
∴f(n)的最大值为f(1)=,f(n)的最小值为f(2)= ,
于是,由①式得a<-(λ+18),<
当a<b3a时,由-b-18=-3a-18,不存在实数满足题目要求;
当b>3a存在实数λ,使得对任意正整数n,都有a<Sn<b,且λ的取值范围是(-b-18,-3a-18)
故知一年内该水库的最大蓄水量是108.32亿立方米
由上表,V(t)在t=8时取得最大值V(8)=8e2+50-108.52(亿立方米).
极大值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com