
10、【解答】(1)由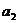 +
+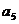 =12,
=12,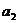
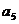 =27,且
=27,且 >0,所以
>0,所以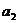 =3,
=3,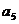 =9,
=9,
∴当t=时取得最小值,最小值为2+3,即k≤2+3. ∴k的取值范围为(-∞,2+3]
f(t)=t-1++1,当t-1∈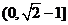 时 f(t)为单调递减函数,
时 f(t)为单调递减函数,
设f(t)==t+=t+=t-1++1.
令t=sinA+cosA,t∈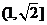 ,
,
∴sinA+sinB的取值范围为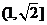 .
.
(Ⅱ)在直角△ABC中, a=csinA,b=ccosA.
若a2(b+c)+b2(c+a)+c2(a+b)≥kabc,对任意的满足题意的a、b、c都成立,
则有≥k,对任意的满足题意的a、b、c都成立,
∵
=[c2sin2A(ccosA+c)+c2cos2A(csinA+c)+c2(csinA+ccosA)]
=[ sin2AcosA+cos2A sinA+1+cosA+sinA]=cosA+sinA+
即()2=?+?,即?=0.∴△ABC 是以C为直角顶点的直角三角形.
∴sinA+sinB=sinA+cosA=sin(A+),A∈(0,) ,
9、【解答】(Ⅰ)∵()2=?+?+?,∴ ()2=?(+)+? ,
∴Dξ=50×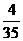 +60×
+60×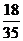 +70×
+70×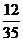 +80×
+80×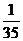 =
=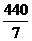 (元).?即该顾客获奖的期望是
(元).?即该顾客获奖的期望是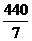 ≈63(元).??
≈63(元).??
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com