
科目:小学数学 来源: 题型:022
(1)从平行四边形一条边上的一点到对边引一条垂线,这点和( )之间的( )叫做平行四边形的高,垂足所在的边叫做平行四边形的( )。
(2)平行四边形具有( )特性,如伸缩门就是运用了这个特性。
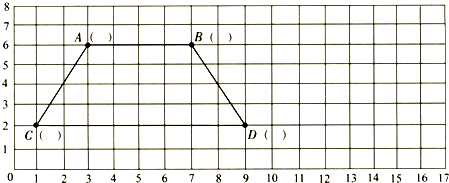
(3)下图是一个平行四边形,可以画出( )条高,其中AB边上的高是( )厘米。

(4)小明把一个长方形拉成了一个平形四边形,平行四边形的周长( )原来长方形的周长,平行四边形的高( )原来长方形的宽。(填“等于”“大于”或“小于”)?
科目:小学数学 来源: 题型:
科目:小学数学 来源: 题型:
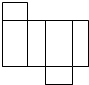 B、
B、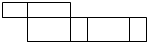 C、
C、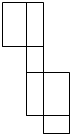 D、
D、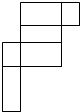
科目:小学数学 来源: 题型:解答题
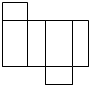 B、
B、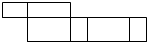 C、
C、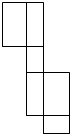 D、
D、
科目:小学数学 来源: 题型:解答题
科目:小学数学 来源: 题型:阅读理解
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com