
科目:小学数学 来源: 题型:单选题
科目:小学数学 来源: 题型:
科目:小学数学 来源:数学教研室 题型:072
(1)
工人师傅利用边角余料铺地板时,用六个形状一样的三角形拼在一起,能够无缝隙地覆盖住A点及其周围小区域,用四个形状一样的四边形拼在一起,也能无缝隙地盖住A点及其周围小区域,从上述的两种覆盖中,我们发现:要完全盖住A点及其周围小区域,必须满足的条件是:拼在A处并以A为顶点的几个角的度数和为________。用边长相等、各角相等的正五边形不能覆盖住A点及其周围小区域的理由是:________之和小于360°,而________之和________360°。(2)
有边数分别为x、y、z,型号不同的多边形,且每种型号的多边形均满足各边相等、各角相等;如果每种型号的多边形各取一个,拼在A点,恰好能覆盖住A点及其周围小区域,请你提出一个关于x、y、z之间关系的猜想,并加以证明。科目:小学数学 来源: 题型:
 于心在圆柱体的金鱼缸的缸口贴了一圈装饰花边(见图1).她用正六边形和等边三角形按图2的样式进行密铺.
于心在圆柱体的金鱼缸的缸口贴了一圈装饰花边(见图1).她用正六边形和等边三角形按图2的样式进行密铺.科目:小学数学 来源: 题型:解答题
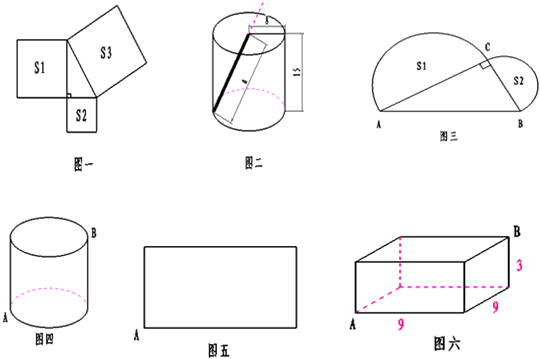
科目:小学数学 来源: 题型:阅读理解
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com