
科目:小学数学 来源: 题型:阅读理解
科目:小学数学 来源: 题型:041
读一读、想一想、说一说.
生活中有些事情一定发生
(比如,每天太阳都是从东面升起).有些事情可能发生,也可能不发生
(比如,天阴了,但是不一定下雨),而且可能性有大有小(小明已经迟到半小时了,今天来的可能性不大了).有时,可能性还会恰好相等.我们不妨做一个掷硬币的实验.
在掷硬币之前,我们可以设想当硬币从空中落下来以后,会出现哪几种情况.



真的会有这三种情况吗?让我们试一试,实践是检验真理的客观标准.
下表是五位著名的学者分别实验的结果.
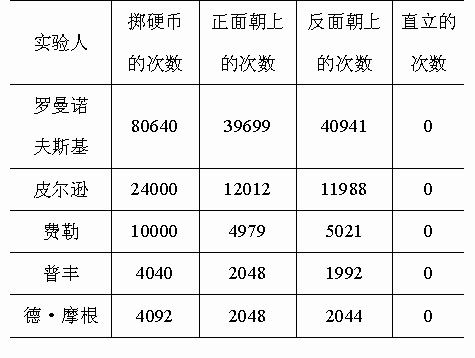
你发现上表中的数据有什么特点?


科目:小学数学 来源:数学教研室 题型:039
读一读、想一想、说一说.
生活中有些事情一定发生
(比如,每天太阳都是从东面升起).有些事情可能发生,也可能不发生
(比如,天阴了,但是不一定下雨),而且可能性有大有小(小明已经迟到半小时了,今天来的可能性不大了).有时,可能性还会恰好相等.我们不妨做一个掷硬币的实验.
在掷硬币之前,我们可以设想当硬币从空中落下来以后,会出现哪几种情况.



真的会有这三种情况吗?让我们试一试,实践是检验真理的客观标准.
下表是五位著名的学者分别实验的结果.
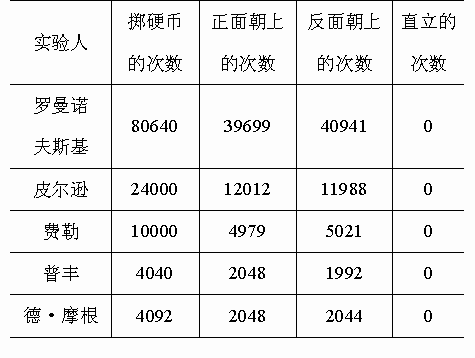
你发现上表中的数据有什么特点?


科目:小学数学 来源:新课标三维同步训练与评价 数学(人教版·小学一年级上册) 题型:071
理解下面的小知识,说一说,太阳早晨比中午离我们更近吗?
太阳早晨比中午离我们更近吗?
生活中我们都有这样一种感觉:早晨的太阳看起来比中午大些,这是不是太阳早晨比中午离我们更近呢?
如果我们用一架调好的照相机各拍一张早晨和中午的太阳,比较一下便会发现它们的大小是完全一样的,那为什么我们看到的并不一样呢?
原来我们的眼睛在观察物体时,感觉到的大小不仅取决于物体本身的实际大小,另外还受距离远近、背景衬托以及物体本身亮度等诸多因素的影响,有时我们会产生错觉.
早晨,太阳刚从地平线升起,由于地平线离我们很远,远处背景中的树木、房屋小得使人看不清楚,太阳在这个背景下从地平线上升起,看起来就显得很大;而中午太阳高挂在广阔的天空,和大地上近处高大的树木和房屋比较,就显得很小.
早晨,太阳刚刚从地平线升起,这时大地还处在比较昏暗的状态,明亮的太阳在暗淡的背景中就会显得特别大些,而中午高悬在天空中的太阳和周围明亮的天空相比亮度相差较小,光渗现象不显著,看起来就觉得小了.
早晨所见太阳之所以比中午显得大些,还有一个原因,那就是早晨太阳位置低,我们观察时眼睛是平视的,眼球中的晶状体保持正常的状态,凸起程度较小,焦距较大,太阳透过晶状体在视网膜上成的像也较大.而中午我们观察太阳需要抬头仰视,又由于受头颈弯曲程度的限制,太阳光不能直射进入人眼,我们看太阳是斜视的,为在视网膜上得到清晰的像,晶状体便会不由自主地凸起来,使其焦距变小,在视网膜上所成的像也会变小些,所以仰视时会觉得太阳小些.
如果我们中午躺在地上戴着太阳镜看太阳,会觉得比站着时稍大些.
由此可看出,我们之所以感觉早晨的太阳比中午大,并不是由于太阳离我们距离的远近造成的(这个距离的影响实在太小了),其中主要原因是由我们的错觉造成的.
科目:小学数学 来源: 题型:阅读理解
科目:小学数学 来源:辽宁省同步题 题型:单选题
阅读下面资料,然后回答问题。
我们所生活的地球应当叫水球,因为地球 面积的被水占着。地球拥有的水量非常巨大,总量为13.86亿立方千米,而其中的96.5%在海洋里;1.76%在冰川、冻土、雪盖中,是固体状态;1.7010在地下;余下的分散在湖泊、江河、大气和生物体中。可以说,从天上到地下,从陆地到海洋,到处都是水。
面积的被水占着。地球拥有的水量非常巨大,总量为13.86亿立方千米,而其中的96.5%在海洋里;1.76%在冰川、冻土、雪盖中,是固体状态;1.7010在地下;余下的分散在湖泊、江河、大气和生物体中。可以说,从天上到地下,从陆地到海洋,到处都是水。
但是,地球上的水尽管数量巨大,、而能直接被人们生产和生活利用的,却少得可怜。首先,海水又咸又苦,不能饮用,不能浇地,也难以用于工业。其次,淡水只占总水量的2.6010左右,其中的绝大部分(占99%)被冻结在远离人类的南北两极和冻土中,无法利用, 只有不到 的淡水,它们散布在湖泊里、江河中和地底下。与全世界总水体比较起来,可以使用的淡水量真如九牛一毛。
的淡水,它们散布在湖泊里、江河中和地底下。与全世界总水体比较起来,可以使用的淡水量真如九牛一毛。
我国的水资源短缺,由来以久。在2200多年的历史文献记载中,发生大的旱灾就达1300次之多。我国水资源人均占有量只有□立方米左右,约为世界人均水量的四分之一。我国水资源不仅人均占有量少,而且水资源分布极不均匀,长江以北水系流域面积占国土面积的63.5%,水资源却占全国的19%。随着我国社会和经济的发展,水的缺口也越来越大。目前我国农业灌溉每年平均缺水300多亿立方米, 全国农村还有3000多万人饮水困难。全国有400多个城市缺水,严重缺水的城市有 个, 全国城市日缺水量为1600万立方米,每年因为缺水影响工业产值( )元以上,影响城市人口( )人。因此在世界水资源正在日趋减少的时候我们更应该注意节约用水,尽量不浪费水资源。
个, 全国城市日缺水量为1600万立方米,每年因为缺水影响工业产值( )元以上,影响城市人口( )人。因此在世界水资源正在日趋减少的时候我们更应该注意节约用水,尽量不浪费水资源。
(1)陆地的面积大约占地球面积的29%,资料中 处应该填入的百分数应该是
处应该填入的百分数应该是
 处应该填入的百分数应该是
处应该填入的百分数应该是 处应该填入
处应该填入科目:小学数学 来源:数学教研室 题型:072
小聪、小明、小慧、小灵、小虎
5个小伙伴是同班同学,也是要好的邻居,他们组成了课外学习小组,经常在王大伯的指导下研究一些生活中的数学问题。一天,王大伯要用一块长
240cm、宽120cm的长方形铁皮,焊接成一个高30cm的长方体无盖水箱,请他们设计一个最省材料的方案。大家都意识到,要做到最省材料就需要想办法增加容积,可不是一件容易的事,商量一下后,大家都认真地画起图来。
性急的小虎马上就想出了办法,他先画出了一个图
(如图),说:“从这个长方形的四个角处各切掉一个边长为30cm的正方形,然后折起四边,就可以得到一个高30cm的水箱啦!”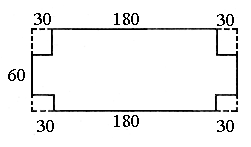
小虎刚说完,小慧就接过话来:“这个方案肯定不理想,浪费了
4个角的材料多可惜!”大家都想不出好的办法,于是个个紧锁眉头在底下胡乱画着,突然小聪大叫起来:“我想出办法了,可以在一边切出两个正方形,然后在对面焊上,这样做成的水箱宽
60cm、高30cm,但长是210cm,而且没有浪费材料,我想容积也一定大了。”小明很快算出了刚才小虎设计的容积大约是
324升,小聪的方案(如图)大约是378升,容积是大多了,而且充分地利用了材料,正当大家为小聪高兴的时候,小灵冷不丁的冒出一句:“这样的容积一定是最大的吗?不浪费不等于最节省啊,既然高已经确定了,我想只有底面积最大容积才最大,最充分的利用材料也就是最节省材料。”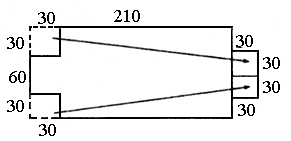
经小灵一提醒,小慧突然想到:“老师说过,周长相等时,正方形的面积最大,应该尽量让底面积做成正方形的。”最后还是小灵想出办法:我们先切下两块长
120cm、宽30cm的长方形,然后在另两边焊上,作为水箱的两个侧面,这样做的水箱底恰好是一个正方形(如图)。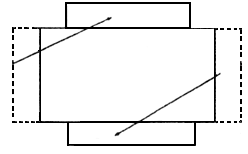
读完上述内容,你看懂了吗
?如果看懂了,请你试着解决下面的问题,你是否还有其他的设计方案,请你动手画一画,算一算:用一张长
30厘米、宽20厘米的长方形铁皮(如图)做一个长方体铁皮盒(焊接处与铁皮厚度不计),做成的铁盒容积是多少立方厘米?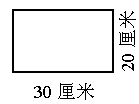
科目:小学数学 来源: 题型:071
叶序现象与斐波那契数列
你吃过菠萝么
?仔细观察菠萝果实的排列状况,就会发现它们形成一种螺旋结构。使人惊异的是,这种排列的现象在植物的叶、鳞片、花等部分,几乎到处可见。再进一步研究一下这些排列的状况,它们通常是以顺时针方向或逆时针方向螺旋形层层排列的。如果数一下其中顺时针和逆时针排列的层数,就可发现这两个数是位于斐波那契数列中相邻的两个数。
什么是斐波那契数列
?斐波那契(1170-1240)是一位意大利的数学家。他在所写的《算盘书》一书中,提出了下面的问题。“有小兔子一对,如果它们第二个月成年,第三个月生下一对小兔,以后,每月生产小兔一对,而所生的小兔亦在第二个月成年,第三个月生产另一对小兔,此后也每个月生一对小兔。则一年后共有多少对兔子
?”(假设每产一对兔子必为一雌一雄,而所有兔子都可以相互交配,并且没有死亡。)
分析:

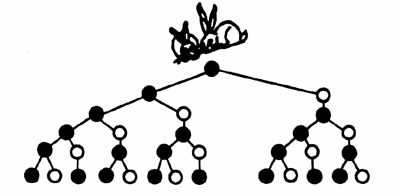
这样推算下去,每个月所生的兔子数可以排成下面的数列:
1,1,2,3,5,8,13,21,34,55,89,144……
我们把这一列数称为斐波那契数列。研究一下这一列数的规律,从第三项起每一个数都是排在它前面两个数的和。如
2=1+1,3=1+2,5=2+3,8=3+5,13=5+8,21=8+13,…
斐波那契数列可以无限地写下去。设
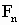 表示其中的第n项,那么
表示其中的第n项,那么
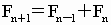 。
。
比如,我们上面排出的第
11项是89,第12项是144,那么第13项应该是
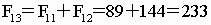
以下各项依序是
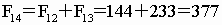
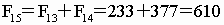
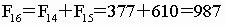
… … …
生物学家研究了花序中小花排列的螺旋数,一般顺时针方向为
21,逆时针方向为34,恰恰是斐波那契数列中的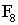 及
及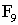 。又如向日葵花序中小花或籽粒的排列,顺时针螺旋数与逆时针螺旋数之比一般是12∶21(
。又如向日葵花序中小花或籽粒的排列,顺时针螺旋数与逆时针螺旋数之比一般是12∶21(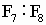 ),34∶55(
),34∶55( ),89∶144(
),89∶144(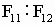 ),在一些大型样本中,这个比值甚至为144∶233(
),在一些大型样本中,这个比值甚至为144∶233(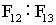 )。同样,生物学家研究了各种菠萝球形花的鳞片顺、逆时针的螺旋数,一般总是落在斐波那契数列3,5,8和13相邻的两数中。
)。同样,生物学家研究了各种菠萝球形花的鳞片顺、逆时针的螺旋数,一般总是落在斐波那契数列3,5,8和13相邻的两数中。
为什么不同的植物都具有类似的螺旋
?为什么这些螺旋圈数总是相邻的斐波那契数?兔子的繁衍与植物的花序之间为什么会有这样的联系,这些问题至今尚未得到令人满意的解答。目前,科学家们一般认为,对植物来说,斐波那契叶序是最节约能量的。科目:小学数学 来源:数学教研室 题型:072
叶序现象与斐波那契数列
你吃过菠萝么
?仔细观察菠萝果实的排列状况,就会发现它们形成一种螺旋结构。使人惊异的是,这种排列的现象在植物的叶、鳞片、花等部分,几乎到处可见。再进一步研究一下这些排列的状况,它们通常是以顺时针方向或逆时针方向螺旋形层层排列的。如果数一下其中顺时针和逆时针排列的层数,就可发现这两个数是位于斐波那契数列中相邻的两个数。
什么是斐波那契数列
?斐波那契(1170-1240)是一位意大利的数学家。他在所写的《算盘书》一书中,提出了下面的问题。“有小兔子一对,如果它们第二个月成年,第三个月生下一对小兔,以后,每月生产小兔一对,而所生的小兔亦在第二个月成年,第三个月生产另一对小兔,此后也每个月生一对小兔。则一年后共有多少对兔子
?”(假设每产一对兔子必为一雌一雄,而所有兔子都可以相互交配,并且没有死亡。)
分析:

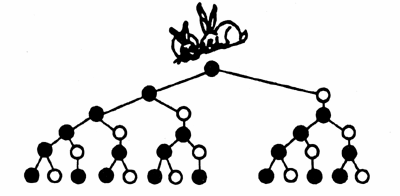
这样推算下去,每个月所生的兔子数可以排成下面的数列:
1,1,2,3,5,8,13,21,34,55,89,144……
我们把这一列数称为斐波那契数列。研究一下这一列数的规律,从第三项起每一个数都是排在它前面两个数的和。如
2=1+1,3=1+2,5=2+3,8=3+5,13=5+8,21=8+13,…
斐波那契数列可以无限地写下去。设
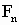 表示其中的第n项,那么
表示其中的第n项,那么
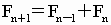 。
。
比如,我们上面排出的第
11项是89,第12项是144,那么第13项应该是
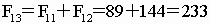
以下各项依序是
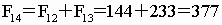
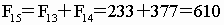
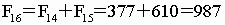
… … …
生物学家研究了花序中小花排列的螺旋数,一般顺时针方向为
21,逆时针方向为34,恰恰是斐波那契数列中的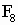 及
及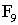 。又如向日葵花序中小花或籽粒的排列,顺时针螺旋数与逆时针螺旋数之比一般是12∶21(
。又如向日葵花序中小花或籽粒的排列,顺时针螺旋数与逆时针螺旋数之比一般是12∶21( ),34∶55(
),34∶55(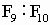 ),89∶144(
),89∶144(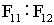 ),在一些大型样本中,这个比值甚至为144∶233(
),在一些大型样本中,这个比值甚至为144∶233( )。同样,生物学家研究了各种菠萝球形花的鳞片顺、逆时针的螺旋数,一般总是落在斐波那契数列3,5,8和13相邻的两数中。
)。同样,生物学家研究了各种菠萝球形花的鳞片顺、逆时针的螺旋数,一般总是落在斐波那契数列3,5,8和13相邻的两数中。
为什么不同的植物都具有类似的螺旋
?为什么这些螺旋圈数总是相邻的斐波那契数?兔子的繁衍与植物的花序之间为什么会有这样的联系,这些问题至今尚未得到令人满意的解答。目前,科学家们一般认为,对植物来说,斐波那契叶序是最节约能量的。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com