| 如图,已知四边形ABCD为⊙O的内接四边形,过点C作CE//AB,交AD的延长线于E,则下列结论中,正确的是 |

|
A.∠BAD+∠BCE=180°
B.∠CDE+∠BCE=180°
C.∠CED+∠BCE=180°
D.∠ADC+∠BCE=180° |
相关习题
科目:初中数学
来源:北京期末题
题型:单选题
如图,已知四边形ABCD为⊙O的内接四边形,过点C作CE//AB,交AD的延长线于E,则下列结论中,正确的是
A.∠BAD+∠BCE=180°
B.∠CDE+∠BCE=180°
C.∠CED+∠BCE=180°
D.∠ADC+∠BCE=180°
查看答案和解析>>
科目:初中数学
来源:
题型:解答题
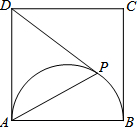 如图,已知四边形ABCD是正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PD.
如图,已知四边形ABCD是正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PD.
(1)若∠PAB=37°,正方形的边长为5,求PA的长度;
(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(2)若PA=PD,过点P作PE⊥AD,垂足为E,判断直线PE与半圆的位置关系并说明理由.
查看答案和解析>>
科目:初中数学
来源:
题型:047
如图,已知圆内接四边形ABCD,延长一组对边DA、CB交于点E,过E作EF∥CD交AB的延长线于F,过F 作圆的切线FG,G为切点,求证EF=FG。

查看答案和解析>>
科目:初中数学
来源:
题型:
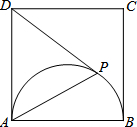
(2013•厦门质检)如图,已知四边形ABCD是正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PD.
(1)若∠PAB=37°,正方形的边长为5,求PA的长度;
(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(2)若PA=PD,过点P作PE⊥AD,垂足为E,判断直线PE与半圆的位置关系并说明理由.
查看答案和解析>>
科目:初中数学
来源:2011年北京市房山区中考数学二模试卷(解析版)
题型:解答题
已知菱形纸片ABCD的边长为8,∠A=60°,E为AB边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点A'处,过点A'作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点C'处,C'G与C'H分别交A'E与A'F于点M、N.若点C'在△A'EF的内部或边上,此时我们称四边形A'MC'N(即图中阴影部分)为“重叠四边形”.
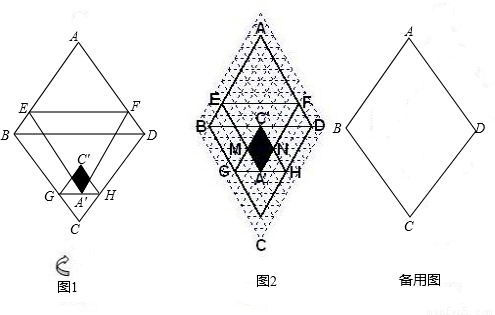
(1)若把菱形纸片ABCD放在菱形网格中(图中每个小三角形都是边长为1的等边三角形),点A、B、C、D、E恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠四边形A'MC'N的面积;
(2)实验探究:设AE的长为m,若重叠四边形A'MC'N存在.试用含m的代数式表示重叠四边形A'MC'N的面积,并写出m的取值范围(直接写出结果,备用图供实验,探究使用).
解:(1)重叠四边形A'MC'N的面积为______
查看答案和解析>>
科目:初中数学
来源:
题型:阅读理解
阅读下列材料,然后解答问题.
经过正四边形(即正方形)各顶点的圆叫作这个正四边形的外接圆,圆心是正四边形的对称中心,这个正四边形叫作这个圆的内接正四边形.
如图,已知正四边形ABCD的外接圆⊙O,⊙O的面积为S
1,正四边形ABCD的面积为S
2,以圆心O为顶点作∠MON,使∠MON=90°,将∠MON绕点O旋转,OM、ON分别与⊙O相交于点E、F,分别与正四边形ABCD的边相交于点G、H.设由OE、OF、
及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
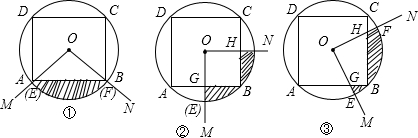
(1)当OM经过点A时(如图①),则S、S
1、S
2之间的关系为:S=
(用含S
1、S
2的代数式表示);
(2)当OM⊥AB时(如图②),点G为垂足,则(1)中的结论仍然成立吗?请说明理由;
(3)当∠MON旋转到任意位置时(如图③),则(1)中的结论仍然成立吗?请说明理由.
查看答案和解析>>
科目:初中数学
来源:
题型:解答题
阅读下列材料,然后解答问题.
经过正四边形(即正方形)各顶点的圆叫作这个正四边形的外接圆,圆心是正四边形的对称中心,这个正四边形叫作这个圆的内接正四边形.
如图,已知正四边形ABCD的外接圆⊙O,⊙O的面积为S1,正四边形ABCD的面积为S2,以圆心O为顶点作∠MON,使∠MON=90°,将∠MON绕点O旋转,OM、ON分别与⊙O相交于点E、F,分别与正四边形ABCD的边相交于点G、H.设由OE、OF、 及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①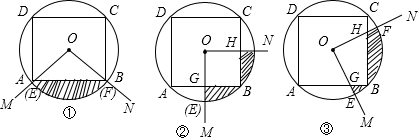
(1)当OM经过点A时(如图①),则S、S1、S2之间的关系为:S=______(用含S1、S2的代数式表示);
(2)当OM⊥AB时(如图②),点G为垂足,则(1)中的结论仍然成立吗?请说明理由;
(3)当∠MON旋转到任意位置时(如图③),则(1)中的结论仍然成立吗?请说明理由.
查看答案和解析>>
科目:初中数学
来源:第24章《圆(下)》中考题集(53):24.4 圆的有关计算(解析版)
题型:解答题
阅读下列材料,然后解答问题.
经过正四边形(即正方形)各顶点的圆叫作这个正四边形的外接圆,圆心是正四边形的对称中心,这个正四边形叫作这个圆的内接正四边形.
如图,已知正四边形ABCD的外接圆⊙O,⊙O的面积为S
1,正四边形ABCD的面积为S
2,以圆心O为顶点作∠MON,使∠MON=90°,将∠MON绕点O旋转,OM、ON分别与⊙O相交于点E、F,分别与正四边形ABCD的边相交于点G、H.设由OE、OF、
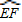
及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
(1)当OM经过点A时(如图①),则S、S
1、S
2之间的关系为:S=______(用含S
1、S
2的代数式表示);
(2)当OM⊥AB时(如图②),点G为垂足,则(1)中的结论仍然成立吗?请说明理由;
(3)当∠MON旋转到任意位置时(如图③),则(1)中的结论仍然成立吗?请说明理由.
查看答案和解析>>
科目:初中数学
来源:第35章《圆(二)》中考题集(40):35.5 圆与圆的位置关系(解析版)
题型:解答题
阅读下列材料,然后解答问题.
经过正四边形(即正方形)各顶点的圆叫作这个正四边形的外接圆,圆心是正四边形的对称中心,这个正四边形叫作这个圆的内接正四边形.
如图,已知正四边形ABCD的外接圆⊙O,⊙O的面积为S
1,正四边形ABCD的面积为S
2,以圆心O为顶点作∠MON,使∠MON=90°,将∠MON绕点O旋转,OM、ON分别与⊙O相交于点E、F,分别与正四边形ABCD的边相交于点G、H.设由OE、OF、
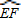
及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
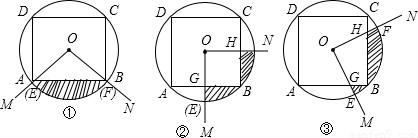
(1)当OM经过点A时(如图①),则S、S
1、S
2之间的关系为:S=______(用含S
1、S
2的代数式表示);
(2)当OM⊥AB时(如图②),点G为垂足,则(1)中的结论仍然成立吗?请说明理由;
(3)当∠MON旋转到任意位置时(如图③),则(1)中的结论仍然成立吗?请说明理由.
查看答案和解析>>
科目:初中数学
来源:第3章《圆》中考题集(80):3.4 弧长和扇形的面积,圆锥的侧面展开图(解析版)
题型:解答题
阅读下列材料,然后解答问题.
经过正四边形(即正方形)各顶点的圆叫作这个正四边形的外接圆,圆心是正四边形的对称中心,这个正四边形叫作这个圆的内接正四边形.
如图,已知正四边形ABCD的外接圆⊙O,⊙O的面积为S
1,正四边形ABCD的面积为S
2,以圆心O为顶点作∠MON,使∠MON=90°,将∠MON绕点O旋转,OM、ON分别与⊙O相交于点E、F,分别与正四边形ABCD的边相交于点G、H.设由OE、OF、
及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
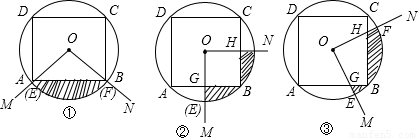
(1)当OM经过点A时(如图①),则S、S
1、S
2之间的关系为:S=______(用含S
1、S
2的代数式表示);
(2)当OM⊥AB时(如图②),点G为垂足,则(1)中的结论仍然成立吗?请说明理由;
(3)当∠MON旋转到任意位置时(如图③),则(1)中的结论仍然成立吗?请说明理由.
查看答案和解析>>

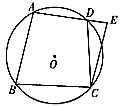
 如图,已知四边形ABCD是正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PD.
如图,已知四边形ABCD是正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PD.
 (2013•厦门质检)如图,已知四边形ABCD是正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PD.
(2013•厦门质检)如图,已知四边形ABCD是正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PD.


 及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
 及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
 及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
 及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①