
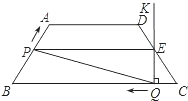
| 如图,在等腰梯形ABCD中,AD∥BC,AB=CD。点P为底边BC的延长线上任意一点,PE⊥AB于E,PF⊥DC于F,BM⊥DC于M。请你探究线段PE、PF、BM之间的数量关系:( )。 |
|
A.PE=PF+BM B.PE>PF+BM C.PE<PF+BM |
科目:初中数学 来源: 题型:
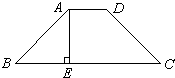 24、如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AE⊥BC于点E,AD=2,AE=3,∠B=45°.
24、如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AE⊥BC于点E,AD=2,AE=3,∠B=45°.科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:
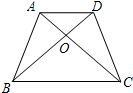 20、如图,在等腰梯形ABCD中,AD∥BC,AB≠AD,对角线AC,BD相交于点O.如下四个结论:
20、如图,在等腰梯形ABCD中,AD∥BC,AB≠AD,对角线AC,BD相交于点O.如下四个结论:科目:初中数学 来源: 题型:
 写出t的取值范围)
写出t的取值范围)科目:初中数学 来源: 题型:
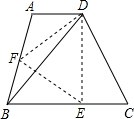 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠DBC=45°,点F在AB边上,点E在BC边上,将△BFE沿折痕EF翻折,使点B落在点D处.若AD=1,BC=5.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠DBC=45°,点F在AB边上,点E在BC边上,将△BFE沿折痕EF翻折,使点B落在点D处.若AD=1,BC=5.科目:初中数学 来源: 题型:
| 2 |
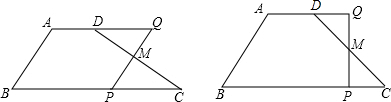
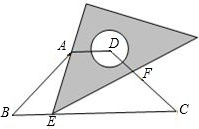 点E在边BC上移动,一直角边始终经过点A,斜边与腰CD(或CD的延长线)交于点F.设BE=x,CF=y.
点E在边BC上移动,一直角边始终经过点A,斜边与腰CD(或CD的延长线)交于点F.设BE=x,CF=y.科目:初中数学 来源: 题型:
 17、如图,在等腰梯形ABCD中,AD∥BC,AB=CD.
17、如图,在等腰梯形ABCD中,AD∥BC,AB=CD.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com