科目：初中数学 来源： 题型：

直角梯形ABCD中，AB∥CD，∠A=30°，AB+CD=m，BC+AD=n，则梯形ABCD的面积为（　　）

A、

1

4

mn

B、

1

5

mn

C、

1

6

mn

D、

1

8

mn

查看答案和解析>>

科目：初中数学 来源：不详 题型：单选题

直角梯形ABCD中，AB∥CD，∠A=30°，AB+CD=m，BC+AD=n，则梯形ABCD的面积为（　　）

A．

1

4

mn

B．

1

5

mn

C．

1

6

mn

D．

1

8

mn

查看答案和解析>>

科目：初中数学 来源： 题型：单选题

直角梯形ABCD中，AB∥CD，∠A=30°，AB+CD=m，BC+AD=n，则梯形ABCD的面积为

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

查看答案和解析>>

科目：初中数学 来源：同步题 题型：单选题

[ ]

A．

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2a，CD=a，BC=2，四边形BEFG是矩形，点E

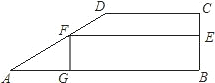、F分别在腰BC、AD上，点G在AB上．设FG=x，矩形BEFG的面积为y．
（1）求y关于x的函数关系式；
（2）当矩形BEFG的面积等于梯形ABCD的面积的一半时，求x的值；
（3）当∠DAB=30°时，矩形BEFG是否能成为正方形？若能，求其边长；若不能，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

如图，在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2a，CD=a，BC=2，四边形BEFG是矩形，点E、F分别在腰BC、AD上，点G在AB上．设FG=x，矩形BEFG的面积为y．
（1）求y关于x的函数关系式；
（2）当矩形BEFG的面积等于梯形ABCD的面积的一半时，求x的值；
（3）当∠DAB=30°时，矩形BEFG是否能成为正方形？若能，求其边长；若不能，请说明理由．

查看答案和解析>>

科目：初中数学 来源：广东省中考真题 题型：解答题

如图，在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2a，CD=a，BC=2，四边形BEFG是矩形，点E、F分别在腰BC、AD上，点G在AB上。设FG=x，矩形BEFG的面积为y。

（1）求y关于x的函数关系式；
（2）当矩形BEFG的面积等于梯形ABCD的面积的一半时，求x的值；
（3）当∠DAB=30°时，矩形BEFG是否能成为正方形，若能，求其边长；若不能，请说明理由。

查看答案和解析>>

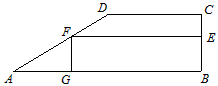
科目：初中数学 来源：第2章《二次函数》中考题集（37）：2.7 最大面积是多少（解析版） 题型：解答题

如图，在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2a，CD=a，BC=2，四边形BEFG是矩形，点E、F分别在腰BC、AD上，点G在AB上．设FG=x，矩形BEFG的面积为y．
（1）求y关于x的函数关系式；
（2）当矩形BEFG的面积等于梯形ABCD的面积的一半时，求x的值；
（3）当∠DAB=30°时，矩形BEFG是否能成为正方形？若能，求其边长；若不能，请说明理由．

查看答案和解析>>

科目：初中数学 来源：第34章《二次函数》中考题集（40）：34.4 二次函数的应用（解析版） 题型：解答题

如图，在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2a，CD=a，BC=2，四边形BEFG是矩形，点E、F分别在腰BC、AD上，点G在AB上．设FG=x，矩形BEFG的面积为y．
（1）求y关于x的函数关系式；
（2）当矩形BEFG的面积等于梯形ABCD的面积的一半时，求x的值；
（3）当∠DAB=30°时，矩形BEFG是否能成为正方形？若能，求其边长；若不能，请说明理由．

查看答案和解析>>

科目：初中数学 来源：第2章《二次函数》中考题集（39）：2.3 二次函数的应用（解析版） 题型：解答题

如图，在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2a，CD=a，BC=2，四边形BEFG是矩形，点E、F分别在腰BC、AD上，点G在AB上．设FG=x，矩形BEFG的面积为y．
（1）求y关于x的函数关系式；
（2）当矩形BEFG的面积等于梯形ABCD的面积的一半时，求x的值；
（3）当∠DAB=30°时，矩形BEFG是否能成为正方形？若能，求其边长；若不能，请说明理由．

查看答案和解析>>

练习册

高中

初中

小学

直角梯形ABCD中，AB∥CD，∠A=30°，AB+CD=m，BC+AD=n，则梯形ABCD的面积为