
科目:初中数学 来源: 题型:
| c |
| a |
| a2b2 |
| c2 |
| 2 |
| c |
| 1 |
| a2b2 |
| 2ab |
| c2 |
| 2 |
| abc |
| 2 |
| ab |
| 2ab |
| c |
| 101 |
| c |
科目:初中数学 来源:不详 题型:填空题
| c |
| a |
| a2b2 |
| c2 |
| 2 |
| c |
| 1 |
| a2b2 |
| 2ab |
| c2 |
| 2 |
| abc |
| 2 |
| ab |
| 2ab |
| c |
| 101 |
| c |
科目:初中数学 来源: 题型:
| S1 | S2 |
科目:初中数学 来源:第27章《相似》中考题集(28):27.2 相似三角形(解析版) 题型:解答题
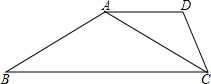
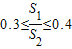 时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.
时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.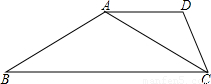
科目:初中数学 来源:2010-2011学年安徽省亳州市蒙城六中九年级(上)第三次月考数学试卷(解析版) 题型:解答题
 时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.
时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.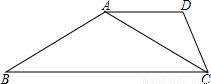
科目:初中数学 来源:第19章《相似形》中考题集(16):19.6 相似三角形的性质(解析版) 题型:解答题
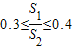 时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.
时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.
科目:初中数学 来源:第29章《相似形》中考题集(20):29.5 相似三角形的性质(解析版) 题型:解答题
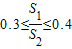 时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.
时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com