
| 点A在数轴上-3的位置,若A沿数轴移动6个单位长度后到达点B,则点B表示的数为 |
A.-9 B.3 C.3或-9 D.不能确定 |
科目:初中数学 来源: 题型:
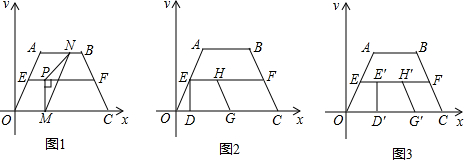
科目:初中数学 来源:2011-2012学年北京市101中学下学期七年级期中考试数学试卷(带解析) 题型:解答题
类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位。用有理数加法表示为3+(-2)=1。 若坐标平面上的点做如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移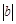 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为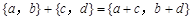 。
。
解决问题:
【小题1】计算:{3,1}+{1,-2};
【小题2】动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗? 在图1中画出四边形OABC。
【小题3】如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程。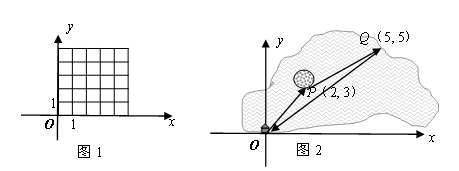
科目:初中数学 来源:2014届北京市下学期七年级期中考试数学试卷(解析版) 题型:解答题
类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位。用有理数加法表示为3+(-2)=1。 若坐标平面上的点做如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为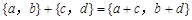 。
。
解决问题:
1.计算:{3,1}+{1,-2};
2.动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗? 在图1中画出四边形OABC。
3.如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程。

科目:初中数学 来源: 题型:解答题

科目:初中数学 来源:同步题 题型:解答题
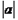 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移 个单位),则把有序数对{a,b}叫做这一平移的“平移量”{a,b}与“平移量”{c,d}的加法运算法则为 {a,b}+{c,d}={a+c,b+d}. 解决问题:
个单位),则把有序数对{a,b}叫做这一平移的“平移量”{a,b}与“平移量”{c,d}的加法运算法则为 {a,b}+{c,d}={a+c,b+d}. 解决问题: 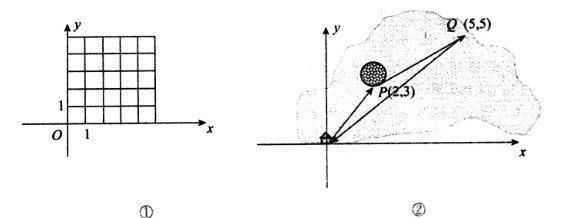
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com