
科目:初中数学 来源: 题型:
在方程3x+4y=16中,当x=3时,y=________,当y=-2时,x=_______ 若x、y都是正整数,那么这个方程的解为___________;
科目:初中数学 来源:同步单元练习北师大版数学九年级上册 题型:022
“解方程x4-6x2+5=0”,这是一个一元四次方程,根据该方程的特点,它的解法通常是:设x2=y,那么,x4=y2,于是原方程可变化为y2-6y+5=0,解这个方程,得:y1=1,y2=5.当y1=1时,x2=1,所以x=±1,当y2=5时,x2=5,所以x=±![]() .所以原方程共有四个根:x1=-1,x2=1,x3=-
.所以原方程共有四个根:x1=-1,x2=1,x3=-![]() ,x4=
,x4=![]() .仿照上面的方法解方程(x2-x)2-4(x2-x)-12=0,若设x2-x=y,则原方程可化为________,原方程的根为________.
.仿照上面的方法解方程(x2-x)2-4(x2-x)-12=0,若设x2-x=y,则原方程可化为________,原方程的根为________.
科目:初中数学 来源:中华题王 数学 九年级上 (北师大版) 北师大版 题型:022
阅读下面解方程的过程,
解方程x4-6x2+5=0
解:设x2=y,那么x4=y2,于是原方程化为
y2-6y+5=0……①
解得y1=1,y2=5,当y1=1时,x2=1,∴x=±1.
当y2=5时,x2=5.∴x=±![]() 所以原方程有四
所以原方程有四
个根是±1,±![]()
(1)在由原方程得到方程①的过程中,利用________法达到降次的目的,体现了转化的数学思想.
(2)解方程(x2-x)2-4(x2-x)-12=0时,若设x2-z=y,则原方程可化为________.
科目:初中数学 来源: 题型:
如图1,矩形![]() 的顶点
的顶点![]() 为原点,点
为原点,点![]() 在
在![]() 上,把
上,把![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,点
处,点![]() 坐标分别为
坐标分别为![]() 和
和![]() ,抛物线
,抛物线![]() 过点
过点![]() .
.
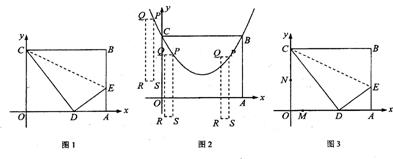
1.求![]() 两点的坐标及该抛物线的解析式;
两点的坐标及该抛物线的解析式;
2.如图2,长、宽一定的矩形![]() 的宽
的宽![]() ,点
,点![]() 沿(1)中的抛物线滑动,在滑动过程中
沿(1)中的抛物线滑动,在滑动过程中![]() 轴,且
轴,且![]() 在
在![]() 的下方,当
的下方,当![]() 点横坐标为-1时,点
点横坐标为-1时,点![]() 距离
距离![]() 轴
轴![]() 个单位,当矩形
个单位,当矩形![]() 在滑动过程中被
在滑动过程中被![]() 轴分成上下两部分的面积比为2:3时,求点
轴分成上下两部分的面积比为2:3时,求点![]() 的坐标;
的坐标;
3.如图3,动点![]() 同时从点
同时从点![]() 出发,点
出发,点![]() 以每秒3个单位长度的速度沿折线
以每秒3个单位长度的速度沿折线![]() 按
按![]() 的路线运动,点
的路线运动,点![]() 以每秒8个单位长度的速度沿折线
以每秒8个单位长度的速度沿折线![]() 按
按![]() 的路线运动,当
的路线运动,当![]() 两点相遇时,它们都停止运动.设
两点相遇时,它们都停止运动.设![]() 同时从点
同时从点![]() 出发
出发![]() 秒时,
秒时,![]() 的面积为
的面积为![]() .①求出
.①求出![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围:②设
的取值范围:②设![]() 是①中函数
是①中函数![]() 的最大值,那么
的最大值,那么![]() = .
= .
科目:初中数学 来源: 题型:
 的顶点
的顶点 为原点,点
为原点,点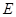 在
在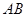 上,把
上,把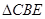 沿
沿 折叠,使点
折叠,使点 落在
落在 边上的点
边上的点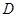 处,点
处,点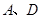 坐标分别为
坐标分别为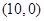 和
和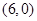 ,抛物线
,抛物线 过点
过点 .
.
 两点的坐标及该抛物线的解析式;
两点的坐标及该抛物线的解析式;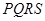 的宽
的宽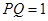 ,点
,点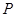 沿(1)中的抛物线滑动,在滑动过程中
沿(1)中的抛物线滑动,在滑动过程中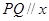 轴,且
轴,且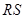 在
在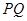 的下方,当
的下方,当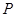 点横坐标为-1时,点
点横坐标为-1时,点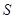 距离
距离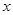 轴
轴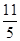 个单位,当矩形
个单位,当矩形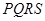 在滑动过程中被
在滑动过程中被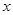 轴分成上下两部分的面积比为2:3时,求点
轴分成上下两部分的面积比为2:3时,求点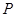 的坐标;
的坐标;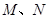 同时从点
同时从点 出发,点
出发,点 以每秒3个单位长度的速度沿折线
以每秒3个单位长度的速度沿折线 按
按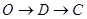 的路线运动,点
的路线运动,点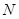 以每秒8个单位长度的速度沿折线
以每秒8个单位长度的速度沿折线 按
按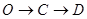 的路线运动,当
的路线运动,当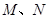 两点相遇时,它们都停止运动.设
两点相遇时,它们都停止运动.设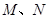 同时从点
同时从点 出发
出发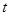 秒时,
秒时, 的面积为
的面积为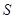 .①求出
.①求出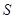 与
与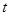 的函数关系式,并写出
的函数关系式,并写出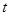 的取值范围:②设
的取值范围:②设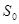 是①中函数
是①中函数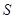 的最大值,那么
的最大值,那么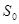 = .
= .科目:初中数学 来源:2011年重庆名校中考数学函数综合试题精练 题型:选择题
如图1,矩形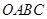 的顶点
的顶点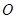 为原点,点
为原点,点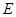 在
在 上,把
上,把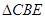 沿
沿 折叠,使点
折叠,使点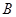 落在
落在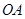 边上的点
边上的点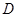 处,点
处,点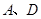 坐标分别为
坐标分别为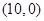 和
和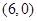 ,抛物线
,抛物线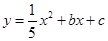 过点
过点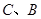 .
.
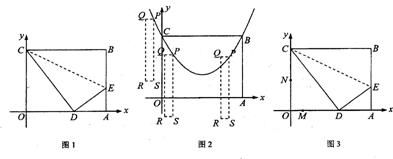
1.求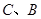 两点的坐标及该抛物线的解析式;
两点的坐标及该抛物线的解析式;
2.如图2,长、宽一定的矩形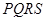 的宽
的宽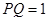 ,点
,点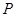 沿(1)中的抛物线滑动,在滑动过程中
沿(1)中的抛物线滑动,在滑动过程中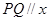 轴,且
轴,且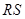 在
在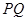 的下方,当
的下方,当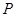 点横坐标为-1时,点
点横坐标为-1时,点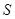 距离
距离 轴
轴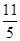 个单位,当矩形
个单位,当矩形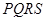 在滑动过程中被
在滑动过程中被 轴分成上下两部分的面积比为2:3时,求点
轴分成上下两部分的面积比为2:3时,求点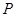 的坐标;
的坐标;
3.如图3,动点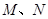 同时从点
同时从点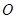 出发,点
出发,点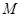 以每秒3个单位长度的速度沿折线
以每秒3个单位长度的速度沿折线 按
按 的路线运动,点
的路线运动,点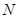 以每秒8个单位长度的速度沿折线
以每秒8个单位长度的速度沿折线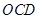 按
按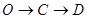 的路线运动,当
的路线运动,当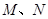 两点相遇时,它们都停止运动.设
两点相遇时,它们都停止运动.设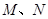 同时从点
同时从点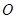 出发
出发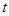 秒时,
秒时,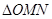 的面积为
的面积为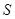 .①求出
.①求出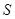 与
与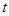 的函数关系式,并写出
的函数关系式,并写出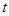 的取值范围:②设
的取值范围:②设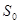 是①中函数
是①中函数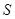 的最大值,那么
的最大值,那么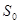 = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com