
科目:初中数学 来源: 题型:阅读理解
| A.好举里巷谐媟以为抚掌之资抚掌:拍手,表示高兴。 |
| B.经营粉本,高下浓淡经营:经度营造 |
| C.不事雕饰,雅合自然雅:文雅 |
| D.尺寸勿爽爽:差错 |
| A.尽其心力以求仿佛赵王岂以一璧之故欺秦邪 |
| B.则李工部之横云之二虫,又何知 |
| C.辄数见焉吴之民方痛心焉 |
| D.与人交,好谈人之善始可与言《诗》已矣 |
| A.本文所记述的张南垣尤擅长垒石造山,具有山水画的意境,构思巧妙,师法自然。 |
| B.本文例举了张南垣所建造园林的代表作及其建造过程,说明他的建造风格,并指出他的技艺符合园林建造的规律。 |
| C.本文还描写了张南垣的外貌性格,因为生得黑而矮胖,又喜欢拿街头巷尾荒唐不经的传说作为谈笑的资料,所以他自己也常常被人调笑耍弄,但他从不与人计较。 |
| D.全文语言流畅工丽,结构严谨,写人状物,如在目前。 |
科目:初中数学 来源: 题型:阅读理解
阅读下列解题过程,借鉴其中一种方法解答后面给出的试题:
问题:某人买13个鸡蛋,5个鸭蛋、9个鹅蛋共用去了9.25元;买2个鸡蛋,4个鸭蛋、3个鹅蛋共用去了3.20元.试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元.
分析:设买鸡蛋,鸭蛋、鹅蛋各一个分别需x、y、z元,则需要求x+y+z的值.由题意,知![]() ;
;
视![]() 为常数,将上述方程组看成是关于y、z的二元一次方程组,化“三元”为“二元”、化“二元”为“一元”从而获解.
为常数,将上述方程组看成是关于y、z的二元一次方程组,化“三元”为“二元”、化“二元”为“一元”从而获解.
解法1:视![]() 为常数,依题意得
为常数,依题意得![]()
解这个关于y、z的二元一次方程组得![]()
于是![]() .
.
评注:也可以视z为常数,将上述方程组看成是关于![]() 、
、![]() 的二元一次方程组,解答方法同上,你不妨试试.
的二元一次方程组,解答方法同上,你不妨试试.
分析:视![]() 为整体,由(1)、(2)恒等变形得
为整体,由(1)、(2)恒等变形得
![]() ,
,
![]() .
.
解法2:设![]() ,
,![]() ,代入(1)、(2)可以得到如下关于
,代入(1)、(2)可以得到如下关于![]() 、
、![]() 的二元一次方
的二元一次方
程组![]()
由⑤+4×⑥,得![]() ,
,![]() .
.
评注:运用整体的思想方法指导解题.视![]() ,
,![]() 为整体,令
为整体,令![]() ,
,![]() ,代人①、②将原方程组转化为关于
,代人①、②将原方程组转化为关于![]() 、
、![]() 的二元一次方程组从而获解.
的二元一次方程组从而获解.
请你运用以上介绍的任意一种方法解答如下数学竞赛试题:
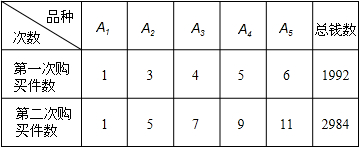
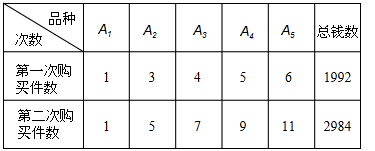
购买五种教学用具A1、A2、A3、A4、A5的件数和用钱总数列成下表:
|
次数 | A1 | A2 | A3 | A4 | A5 | 总钱数 |
| 第一次购 买件数 | l | 3 | 4 | 5 | 6 | 1992 |
| 第二次购 买件数 | l | 5 | 7 | 9 | 11 | 2984 |
那么,购买每种教学用具各一件共需多少元?
科目:初中数学 来源: 题型:解答题
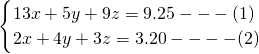 ;
;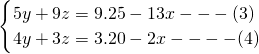 .
.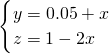 .
.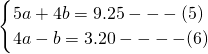 .
.
科目:初中数学 来源:同步题 题型:解答题
 ;
; 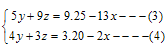
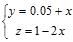
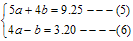
科目:初中数学 来源: 题型:阅读理解
|
|
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com