
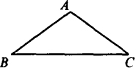
| 已知:如图所示,在△ABC中,∠ ABC=120° ,点E、D分别在AB和AC上,如果AE=ED=DB=BC,求∠A的度数。 |
|
A.60。 B.30。 C.15。 D.7.5。 |
科目:初中数学 来源:1+1轻巧夺冠·优化训练·九年级数学下(北京课改版)·银版 题型:047
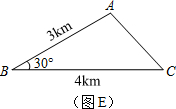
已知:如图所示,在△ABC中,∠BAC=120°,AB=AC,BC=4![]() ,以A为圆心,2为半径作⊙A,试问:
,以A为圆心,2为半径作⊙A,试问:
直线BC与⊙A的关系如何?并证明你的结论.
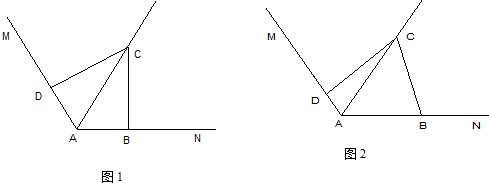
科目:初中数学 来源: 题型:
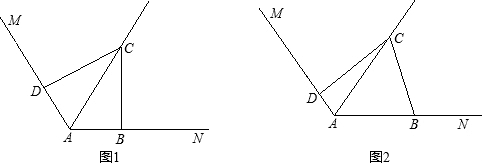
科目:初中数学 来源: 题型:解答题
科目:初中数学 来源: 题型:阅读理解
| 1 | 2 |

科目:初中数学 来源: 题型:解答题
已知:Rt△A′BC′≌Rt△ABC,∠A′C′B=∠ACB=90°,∠A′BC′=∠ABC=60°,Rt△A′BC′可绕点B旋转,设旋转过程中直线CC′和AA′相交于点D.
(1)如图1所示,当点C′在AB边上时,判断线段AD和线段A′D之间的数量关系,并证明你的结论;
(2)将Rt△A′BC′由图1的位置旋转到图2的位置时,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)将Rt△A′BC′由图1的位置按顺时针方向旋转α角(0°≤α≤120°),当A、C′、A′三点在一条直线上时,请直接写出旋转角的度数.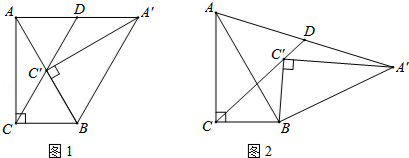
科目:初中数学 来源: 题型:解答题
 DG,其他条件不变,此时,GF是多少?
DG,其他条件不变,此时,GF是多少?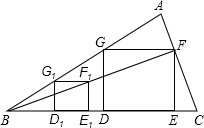
科目:初中数学 来源:广东省月考题 题型:解答题
 DG,其他条件不变,此时,GF是多少?
DG,其他条件不变,此时,GF是多少?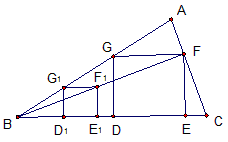
科目:初中数学 来源: 题型:
 |
| BC |
 |
| BC |
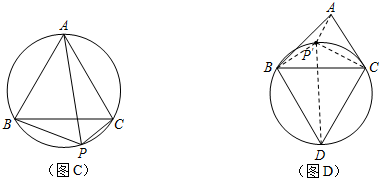
科目:初中数学 来源: 题型:解答题
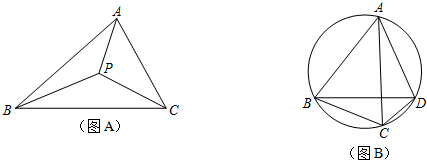
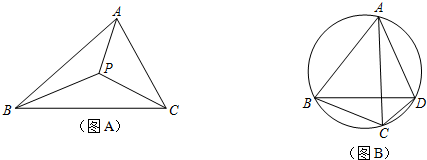
 上任意一点.求证:PB+PC=PA;
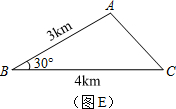
上任意一点.求证:PB+PC=PA; 上任取一点P′,连接P′A、P′B、P′C、P′D.易知P′A+P′B+P′C=P′A+(P′B+P′C)=P′A+______;
上任取一点P′,连接P′A、P′B、P′C、P′D.易知P′A+P′B+P′C=P′A+(P′B+P′C)=P′A+______;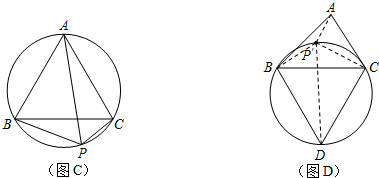
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com