
科目:初中数学 来源:中考数学专项练习 题型:013
在△ABC中,CD是斜边AB上的高,若AC∶BC=1∶![]() ,则△ADC和△CDB面积的比为
,则△ADC和△CDB面积的比为
[ ]
科目:初中数学 来源: 题型:022
在Rt△ABC中,CD是斜边AB上的高,且AC=6cm,BC=8cm,则当以点D为圆心的圆的半径r=________cm时,⊙D与AC相切;r满足条件r________cm时,⊙D与AC相离;r满足条件r________cm时,⊙D与BC相切;r满足条件r________cm时,⊙D与BC相交.
科目:初中数学 来源: 题型:
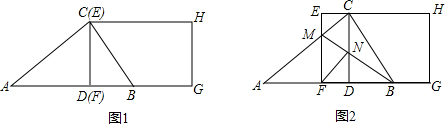
科目:初中数学 来源: 题型:
在△ABC中,∠C=90°,AC=3,BC=4,CD是斜边AB上的高,点E在斜边AB上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.
(1)求线段AD的长;
(2)若EF⊥AB,当点E在线段AB上移动时,
①求y与x的函数关系式(写出自变量x的取值范围)
②当x取何值时,y有最大值?并求其最大值;
(3)若F在直角边AC上(点F与A、C两点均不重合),点E在斜边AB上移动,试问:是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.
科目:初中数学 来源: 题型:
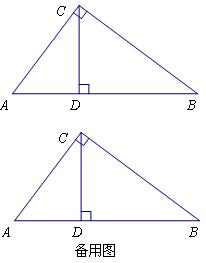
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(江苏扬州) 题型:解答题
在△ABC中,∠C=90°,AC=3,BC=4,CD是斜边AB上的高,点E在斜边AB上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.
(1)求线段AD的长;
(2)若EF⊥AB,当点E在线段AB上移动时,
①求y与x的函数关系式(写出自变量x的取值范围)
②当x取何值时,y有最大值?并求其最大值;
(3)若F在直角边AC上(点F与A、C两点均不重合),点E在斜边AB上移动,试问:是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(江苏常州) 题型:解答题
在△ABC中,∠C=90°,AC=3,BC=4,CD是斜边AB上的高,点E在斜边AB上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.
(1)求线段AD的长;
(2)若EF⊥AB,当点E在线段AB上移动时,
①求y与x的函数关系式(写出自变量x的取值范围)
②当x取何值时,y有最大值?并求其最大值;
(3)若F在直角边AC上(点F与A、C两点均不重合),点E在斜边AB上移动,试问:是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.
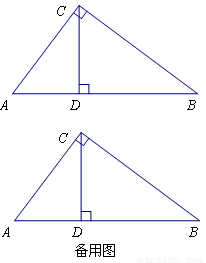
科目:初中数学 来源:2013年吉林省白城市镇赉县胜利中学中考数学四模试卷(解析版) 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com