科目：初中数学 来源： 题型：

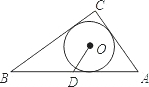如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，⊙O为△ABC的内切圆，点D是斜边AB的中点，则tan∠ODA=（　　）

A、 3 2

B、 3 3

C、 3

D、2

查看答案和解析>>

科目：初中数学 来源： 题型：

10、如图，在Rt△ABC中，∠ACB=90°，AB=2BC，在直线BC或AC上取一点P，使得△PAB为等腰三角形，则符合条件的点P共有（　　）

A、4个

B、5个

C、6个

D、7个

查看答案和解析>>

科目：初中数学 来源： 题型：

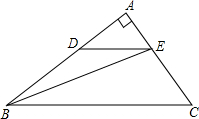如图，在Rt△ABC中，∠A=90°，AB=8，AC=6．若动点D从点B出发，沿线段BA运动到点A为止，运动速度为每秒2个单位长度．过点D作DE∥BC交AC于点E，设动点D运动的时间为x秒，AE的长为y．
（1）求出y关于x的函数关系式，并写出自变量x的取值范围；
（2）求出△BDE的面积S与x之间的函数关系式；
（3）当x为何值时，△BDE的面积S有最大值，最大值为多少？

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，在Rt△ABC中，∠C=90°，O是斜边AB上的一点，圆O过点A并与边BC相切于点D，与边AC相交于点E．
（1）求证：AD平分∠BAC；
（2）若圆O的半径为4，∠B=30°，求AC长．

查看答案和解析>>

科目：初中数学 来源： 题型：

19、如图，在Rt△ABC中，∠B=90°，∠A的平分线交BC于D，E为AB上一点，DE=DC，以D为圆心，以DB的长为半径画圆．
求证：（1）AC是⊙D的切线；（2）AB+EB=AC．

查看答案和解析>>

科目：初中数学 来源： 题型：

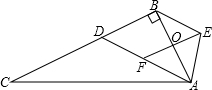如图，在Rt△ABC中，∠ABC=90°，在AB、AC上分别找点E、F，使AE=AF，将△AFE绕点A顺时针方向旋转，EF的中点O恰好落在AB的中点，延长AF交BC于D，连接BE．
（1）四边形BDFE是什么特殊四边形？说明理由．
（2）是否存在Rt△ABC中，使得图中四边形BDFE为菱形？若不存在，说明理由；若存在．求出此时Rt△ABC的面积与△AFE面积的倍数关系．

查看答案和解析>>

科目：初中数学 来源： 题型：

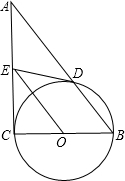如图，在Rt△ABC中，∠C=90°，以BC为直径作⊙O交AB于点D，取AC的中点E，连接DE、OE．
（1）求证：DE是⊙O的切线；
（2）如果⊙O的半径是

3

2

cm，ED=2cm，求AB的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，⊙O为△ABC的内切圆，点D是斜边AB的中点，则tan∠ODA=

 

．

查看答案和解析>>

科目：初中数学 来源： 题型：

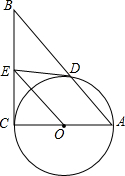如图，在Rt△ABC中，∠C=90°，以AC为直径作圆O，交AB边于点D，过点O作OE∥AB，交BC边于点E．
（1）试判断ED与圆O位置关系，并给出证明；
（2）如果圆O的半径为

3

2

，ED=2，求AB的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

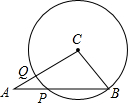如图，在Rt△ABC中，∠C=90°，AC=

2

，BC=1，如果以C为圆心，以CB长为半径的圆交AB于点P，那么AP的长为（　　）

A、 3

B、 3 3

C、 2 3 3

D、3

查看答案和解析>>