如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法正确的是
①ac<0;
②方程ax2+bx+c=0的根是x1=-1;x2=3
③a+b+c>0;
④当x>1时,y 随x的增大而增大;
⑤2a+b>0 |

|
A.③④⑤
B.②③
C.①②④
D.①②③ |
相关习题
科目:初中数学
来源:2010-2011学年江西省南昌市九年级(上)期末数学试卷(二)(解析版)
题型:选择题
如图,抛物线y=ax
2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法正确的是( )
①ac<0;
②方程ax
2+bx+c=0的根是x
1=-1,x
2=3;
③a+b+c>0;
④当x>1时,y随x的增大而增大;
⑤2a+b>0.

A.③④⑤
B.②③
C.①②④
D.①②③
查看答案和解析>>
科目:初中数学
来源:2010-2011学年山东省日照市莒县九年级(上)期末数学试卷(解析版)
题型:选择题
如图,抛物线y=ax
2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法正确的是( )
①ac<0;
②方程ax
2+bx+c=0的根是x
1=-1,x
2=3;
③a+b+c>0;
④当x>1时,y随x的增大而增大;
⑤2a+b>0.

A.③④⑤
B.②③
C.①②④
D.①②③
查看答案和解析>>
科目:初中数学
来源:2010-2011学年江西省宜春市高安四中九年级(上)期末数学试卷(二)(解析版)
题型:选择题
如图,抛物线y=ax
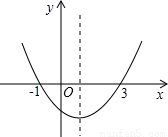
2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法正确的是( )
①ac<0;
②方程ax
2+bx+c=0的根是x
1=-1,x
2=3;
③a+b+c>0;
④当x>1时,y随x的增大而增大;
⑤2a+b>0.
A.③④⑤
B.②③
C.①②④
D.①②③
查看答案和解析>>
科目:初中数学
来源:2010-2011学年江西省宜春市高安四中九年级(上)期末数学试卷(解析版)
题型:选择题
如图,抛物线y=ax
2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法正确的是( )
①ac<0;
②方程ax
2+bx+c=0的根是x
1=-1,x
2=3;
③a+b+c>0;
④当x>1时,y随x的增大而增大;
⑤2a+b>0.

A.③④⑤
B.②③
C.①②④
D.①②③
查看答案和解析>>
科目:初中数学
来源:2009-2010学年天津市大港区九年级(上)期末数学试卷(解析版)
题型:选择题
如图,抛物线y=ax
2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法正确的是( )
①ac<0;
②方程ax
2+bx+c=0的根是x
1=-1,x
2=3;
③a+b+c>0;
④当x>1时,y随x的增大而增大;
⑤2a+b>0.

A.③④⑤
B.②③
C.①②④
D.①②③
查看答案和解析>>
科目:初中数学
来源:
题型:单选题
如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下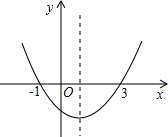 列说法正确的是
列说法正确的是
①ac<0;
②方程ax2+bx+c=0的根是x1=-1,x2=3;
③a+b+c>0;
④当x>1时,y随x的增大而增大;
⑤2a+b>0.
- A.
③④⑤
- B.
②③
- C.
①②④
- D.
①②③
查看答案和解析>>
科目:初中数学
来源:天津期末题
题型:单选题
如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法正确的是
①ac<0; ②方程ax2+bx+c=0的根是x1=-1;x2=3 ③a+b+c>0;④当x>1时,y 随x的增大而增大; ⑤2a+b>0
A.③④⑤
B.②③
C.①②④
D.①②③
查看答案和解析>>
科目:初中数学
来源:
题型:
抛物线y=ax
2+bx+c过点A(-1,0)点B(3,0),其开口向
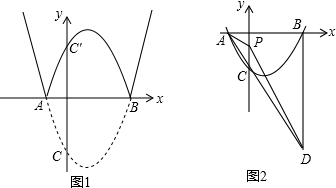
上,点C是抛物线与y轴的交点,且OC=3OA.
(1)求抛物线的解析式;
(2)如图①,将抛物线x轴下方的部分沿x轴对折交y轴于点C,若直线y=-x+b与翻折后的曲线的交点数为两个,求b的取值范围;
(3)如图②,过点B作BD⊥x轴,交AC的延长线于点D,设点C的上方有一点P(0,t),且△PAD的面积为15,若将抛物线沿其对称轴上下平移,使抛物线与△PAD总有公共点,则抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
查看答案和解析>>
科目:初中数学
来源:
题型:解答题
抛物线y=ax2+bx+c过点A(-1,0)点B(3,0),其开口向 上,点C是抛物线与y轴的交点,且OC=3OA.
上,点C是抛物线与y轴的交点,且OC=3OA.
(1)求抛物线的解析式;
(2)如图①,将抛物线x轴下方的部分沿x轴对折交y轴于点C,若直线y=-x+b与翻折后的曲线的交点数为两个,求b的取值范围;
(3)如图②,过点B作BD⊥x轴,交AC的延长线于点D,设点C的上方有一点P(0,t),且△PAD的面积为15,若将抛物线沿其对称轴上下平移,使抛物线与△PAD总有公共点,则抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
查看答案和解析>>
科目:初中数学
来源:2012年湖北省武汉市四月调考逼真模拟数学试卷(一)(解析版)
题型:解答题
抛物线y=ax
2+bx+c过点A(-1,0)点B(3,0),其开口向

上,点C是抛物线与y轴的交点,且OC=3OA.
(1)求抛物线的解析式;
(2)如图①,将抛物线x轴下方的部分沿x轴对折交y轴于点C,若直线y=-x+b与翻折后的曲线的交点数为两个,求b的取值范围;
(3)如图②,过点B作BD⊥x轴,交AC的延长线于点D,设点C的上方有一点P(0,t),且△PAD的面积为15,若将抛物线沿其对称轴上下平移,使抛物线与△PAD总有公共点,则抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
查看答案和解析>>






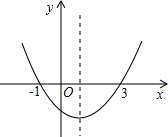 列说法正确的是
列说法正确的是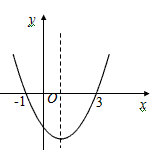
 上,点C是抛物线与y轴的交点,且OC=3OA.
上,点C是抛物线与y轴的交点,且OC=3OA. 上,点C是抛物线与y轴的交点,且OC=3OA.
上,点C是抛物线与y轴的交点,且OC=3OA. 上,点C是抛物线与y轴的交点,且OC=3OA.
上,点C是抛物线与y轴的交点,且OC=3OA.