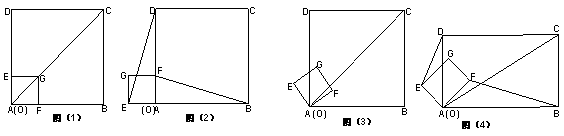
把正方形OFGE纸板按如图①方式放置在正方形纸板ABCD上，顶点G在对角线AC，并把正方形OFGE绕

顶点A沿逆时针方向旋转，旋转角为а。(1)如图②，当а=90°时，请直接写出线段DE与BF的数量关

系和位置关系；(2)如图③，当0°<а<90°时，(1)中的结论是否发生改变？若不变，请给出证明。若发

生改变，请举例说明；(3)如图④，将图①、图③中的两个正方形都改为矩形，其他条件不变，设AB=kAD(k>0)，

当0°<а<90°时，(1)中的结论是否发生改变？若不变，请给出证明。若发生改变，

请写出改变后的新结论，并给出证明。

如图，正方形ABCD中，有一直径为BC的半圆O，BC=2cm，现在两点E、F分别从点B、点A同时出发，点E沿线段BA以1cm/秒的速度向点A运动，点F沿折线A―D―C以2cm/秒的速度向点C运动，设点E离开点B的时间为t秒。

   （1）如图①，当t为何值时，EF//BC，并判断此时EF与半圆O的位置关系（要说明理由）

   （2）当1<t<2时，设四边形BEFC的面积为s（cm²），则s与t的函数关系为           ；

   （3）如图②，设1<t<2，当t为何值时，EF与半圆O相切？

如图，反比例函数(x>0)与一次函数的图象相交于A、B两点，已知当y₂>y₁时，x的取值范围是1<x<3.

（1）求、的值;

（2）求△AOB的面积.

如图，在矩形ABCD中，AB＝6米，BC＝8米，动点P以2米/秒的速度从点A出发，沿AC向点C移动，同时动点Q以1米/秒的速度从点C出发，沿CB向点B移动，设P、Q两点移动t秒（0<t<5）后，四边形ABQP的面积为S米²。

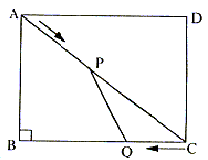
　 （1）求面积S与时间t的关系式；

　 （2）在P、Q两点移动的过程中，四边形ABQP与△CPQ的面积能否相等？若能，求出此时点P的位置；若不能，请说明理由。